2015-10-22
3415
Лекция 3
Здесь будет рассмотрено понятие вероятности, лежащее в основе, как теории вероятностей, так и математической статистики.
Когда мы говорим о происхождении какого-либо случайного события, то всегда подразумеваем большую или меньшую возможность этого. Выпадение снега, например, событие случайное и появление его абсолютно точно предвосхитить нельзя. Однако, возможность появления его зимой очень велика, а появление его летом — почти невероятно. Таким образом, появление какого-либо случайного события в каких-либо определенных условиях имеет различную возможность.
Преодолеет тот или иной спортсмен высоту 180 см? Все зависит от того, подготовлен он соответствующим образом или нет, преодолевал ли он такую высоту ранее на тренировках или нет, имеет ли он опыт участия в соревнованиях, каково его состояние здоровья в данный момент и т. д. Другими словами, возможность преодолеть такую высоту разная у различных спортсменов. Следовательно, случайное событие — преодолеет ли спортсмен высоту 180 см — имеет разную возможность осуществления.
Если разные случайные события имеют различную возможность для осуществления, есть смысл говорить о какой-то числовой характеристике, отражающей факт различной степени возможности появления случайного события.
Такой характеристикой является вероятность—основное понятие теории вероятностей.
Вероятность есть число, характеризующее возможность осуществления случайного события в определенном испытании.
Под испытанием подразумеваем, условия или обстоятельства, при которых осуществляется появление данного события.
Чтобы привести способ вычисления вероятности, нужно дать еще несколько определений и понятий.
Вероятность, как число, обычно вычисляют после того, как произведена серия испытаний. Естественно, в соответствии с основными положениями теории вероятностей, чем большее количество испытаний проведено, тем точнее будет вычислена вероятность.
В проведенной серии испытаний подсчитывают:
1) количество испытаний, имеющих благоприятный для целей задачи исход, то есть количество испытаний, в которых нужное нам событие появилось. Обозначим их число буквой m;
2) количество всех испытаний, имевших место в данной серии. Предполагается, что любой исход этих испытаний не имеет преимуществ перед остальными, т. е. все исходы имеют равные возможности для того, чтобы произойти. Эти исходы испытания называются равновозможными. Обозначим их n.
Вероятность появления случайного события в данном испытании есть частное от деления числа благоприятствующих исходов испытаний (m) на равновозможные (n).
Вероятность обозначается, прописной латинской буквой Р. В скобках рядом с ней пишут обычно букву (как правило, используют латинский алфавит), которая символически обозначает название рассматриваемого случайного события.
Например, Р(А) обозначает: вероятность происхождения события А. Если, возвращаясь к вышеприведенному примеру, условимся преодоление спортсменом высоты обозначать буквой А, то выражение Р(А) в этой конкретной задаче будет означать вероятность того, что спортсмен преодолеет высоту 180 см.
Формула вероятности будет выглядеть следующим образом:
, (15)
где Р(А) —вероятность появления события А в данном испытании; m — количество благоприятствующих исходов испытания; n —количество равновозможных исходов испытаний.
Рассмотрим это на конкретном примере.
Пример 16. Конечной целью серии тренировок пловца является преодоление им дистанции 200 м вольным стилем за время 2.17,0.
После соответствующей подготовки он проплывал эту дистанцию 25 раз. Результаты его такие: 18 раз он показал желаемый результат, в остальных случаях — результат был хуже. Какова вероятность того, что в тех же условиях он преодолеет дистанцию 200 м за нужное время—2.17,0?
Обозначим вероятность искомого случайного события буквой А. Определению подлежит вероятность Р(А).
В соответствии с формулой (15) вероятность события А находится так:
где m — благоприятствующие; n —равновозможные исходы испытаний.
В данном примере благоприятствующих исходов испытаний было 18, то есть n=18.
Равновозможные исходы испытания — это все испытания, имевшие место в данном примере. Их число n =25.
Таким образом, вероятность искомого события находится так:
Р(А) = 0,72—есть числовая характеристика того, что в данном испытании спортсмен преодолеет дистанцию 200 м за 2.17,0.
Вероятность обычно выражается десятичной дробью. В некоторых случаях ее переводят в проценты, для чего полученную десятичную дробь следует умножить на 100%. В данном примере Р(А) = 0,72.100%=72%.
Вероятность еще можно трактовать как степень уверенности в том, что в данном испытании рассматриваемое случайное событие произойдет.
Пример 17. Три группы школьников соревнуются в беге на 100 м. В первой группе 5, во второй — 7, а в третьей — 6 человек. Всего — 18 школьников.
Какова вероятность победы представителей первой, второй и третьей группы, если уровень спортивной подготовки у всех школьников одинаков?
Из условия примера, очевидно, что, скорее всего победителем, будет спортсмен второй группы, так как в ней больше участников. Но это интуитивно. Для определения точной характеристики такого предположения найдем: вероятность победы членами первой группы Р(А), вероятность победы членами второй группы Р(В) и вероятность победы спортсменами третьей группы Р(С).
Для определения Р(А) выясняем: число благоприятствующих исходов испытаний для первой группы m =5, равновозможных — n=18. Вероятность Р(А) находим по формуле (15):
Р(А)= 
= 
Вероятность Р(В):
Р(В)= = 
где число благоприятствующих исходов испытаний m =7, число равновозможных исходов n =18.
Вероятность Р(С):
Р(С)= = 
Таким образом, учитывая исходные условия, вероятности победы первой, второй и третьей групп соответственно равны:
Р(А) = 0,277; Р(В) = 0,388; Р(С)=0,333.
Как и следовало ожидать, шансы на победу у второй группы — наибольшие.
Пример 18. Спортсмен выполняет тройной прыжок, желая достичь результат 14,50 м. Из 20 прыжков в 12 он показал 14,50 м. Какова вероятность того, что на соревнованиях спортсмен достигнет желаемого результата?
m — число благоприятствующих исходов испытаний, m = 12, n — равновозможные исходы, n = 20. Вероятность удачи:
Р(А)= = 
В соответствии с определением, что ясно также из примеров, вероятность, как число, определяется после того, как прошла серия испытаний. Имеется в виду тот факт, что в серии испытаний, которые еще не проведены, но будут иметь место, найденная вероятность появления случайного события будет та же, если будут соблюдены те же условия, что в прошедшей серии испытаний.
Например, определив в примере 16, что вероятность преодоления пловцом дистанции 200 м вольным стилем за время 2.17,0 составляет Р(А) = 0,72, мы нашли величину 0,72 на основании уже прошедших заплывов. Однако мы имеем все основания предполагать, что при тех же условиях: то же состояние здоровья, та же степень подготовленности, та же дистанция, тот же стиль и т. д. вероятность показания 2.17,0—все та же Р(А) = 0,72.
Таким образом, численное значение вероятности, найденное на основании прошедших испытаний, пригодно для применения в различных перспективных ситуациях, где возникает необходимость оценки появления какого-либо случайного события.
Возвратимся к формуле (15) и еще раз проанализируем величины m и n.
Если n —число всех равновозможных исходов испытаний, а m — это число удачных исходов, то очевидно, что m составляет некоторую часть от n.
Действительно, если m =18, а n =25 в примере 16, то 18 благоприятствующих исходов испытаний есть некоторая часть от всех 25 равновозможных.
В связи с этим есть смысл обратить внимание на два крайних условия: 1) если число всех благоприятствующих исходов равно числу всех равновозможных — т=п и 2) если благоприятствующих исходов не было — m=0 — и все испытания есть равновозможные.
В примере16 эти два крайние условия выглядят так:
1) проведено n = 25 испытаний и все 25 оказались удачными m = 25 (во всех 25 испытаниях он показал желаемый результат 2.17,0). В этом случае вероятность Р(А) есть:
Р(А)= = 
Как видно из этого примера, более чем Р(А)=1 получить числа нельзя, т. к. т не может быть более чем 25.
Таким образом, мы получили одно крайнее условие: если m=n, то Р(А) = 1 и выше этого числа оно быть не может.
События, вероятность которых равна единице, называются достоверными в том смысле, что в данном испытании они должны произойти обязательно;
2) произведено n=25 испытаний и ни одно из них не оказалось удачным m=0 (спортсмен ни разу не преодолел дистанцию за время 2.17,0, а показывал результаты хуже). В этом случае искомая вероятность есть:
Р(А)= = 
Меньше числа 0 вероятность быть не может, так как рассмотрены уже все испытания и ни одно не удалось.
События, вероятность которых равна нулю, называются невозможными в том смысле, что в данном испытании они никогда не произойдут.
Таким образом, в крайних положениях вероятность равна нулю и единице. Во всех прочих случаях она будет принимать значения между нулем и единицей. Записывают это так:
, (16)
то есть значение вероятности колеблется в пределах от нуля до единицы.
Числовой интервал от нуля до единицы дает возможность ориентироваться в оценке величины вероятности.
Крайние два значения определяют вероятности невозможных и достоверных событий. Все остальные характеризуют вероятности событий, появление которых возможно в большей или меньшей степени. Учитывай приведенный интервал, можно считать, что Р(А) = 0,7÷1,0 характеризует большую вероятность, т. е. высокую степень уверенности в том, что данное событие произойдет; Р(А)=0,4÷0,6 дает представление о средней возможности появления события, а Р(А)=0,1÷0,3 — об очень малой степени возможности появления данного события.
Так, в примере 16 Р(А) = 0,72, следовательно, вероятность преодолеть дистанцию 200 м вольным стилем за 2.17,0 высока. Возможность совершить тройной прыжок ]4,5 м спортсменом равна Р(А)=0,6 (средняя вероятность).
Этот же показатель можно получить при оценке всех вероятностей в процентах.
Нахождение численного значения вероятности Р(А) по формуле (15) позволяет ориентироваться в простейших вероятностных ситуациях. Можно, например, знать, какие шансы у спортсмена победить в соревнованиях, чего уже достиг спортсмен в тренировках и как можно улучшить, рассчитать элементарные игровые позиции и т. д.
Более сложные вероятностные ситуации описываются не одним понятием вероятности, а целыми уравнениями, в которые Р(А) входит как составная часть.
Возвратимся еще раз к вышеприведенной формуле (15): Р(А)=
Знаменатель ее есть количество равновозможных исходов испытаний. В самом этом названии кроется смысл и существо данного определения. Равновозможный—тот, который имеет равные возможности, чтобы произойти. Таким образом, определение вероятности по формуле (15) справедливо лишь в том случае, если все исходы испытаний, имевшие место в данной серии, имеют равные шансы появиться. Если бы мы рассмотрели каких-либо 100 испытаний неравновозможных, т. е. не имеющих равных шансов на появление, и из них каких-либо 25 интересующих нас произошли, то вычисление по формуле (15) Р(А)= = 
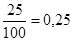не соответствовало бы истинному положению дел и эти вычисления были бы несправедливы.
Рассмотренное обстоятельство очень затрудняет работу над вероятностными процессами.
Возвращаясь к реальным вероятностным ситуациям, обратим внимание на то, что добиться «чистой» равной возможности в появлении каких-либо случайных явлений или процессов весьма сложно. В частности, это можно наблюдать в спорте. Так, в примере 16 мы рассмотрели 25 равновозможных попыток спортсмена преодолеть дистанцию 200 м вольным стилем за время 2.17,0. Однако, строго говоря, все 25 попыток не были равновозможными, так как они могли отличаться друг от друга различной степенью подготовленности спортсмена (например, 25-я попытка могла быть лучше 1-й и т.д.), его состоянием здоровья, настроением, внешними условиями и др. Таким образом, решая задачу на основании n=25 равновозможных исходов испытаний, мы внесли в нее заведомо упрощающее условие, за счет чего, по-видимому, снизили точность окончательного ответа.
В примере 17 было рассмотрено 18 равновозможных участников соревнований. Однако, и в этом случае в таком предположении нет никакой гарантии.
В примере 18 можно также выразить сомнения по поводу принятой равновозможности, т. к. 20 прыжков не всегда строго повторяют друг друга, отличаясь друг от друга усилиями при отталкивании спортсмена, разбегом и т. д.
Таким образом, даже в простейших ситуациях пользование формулой (15) приближается к истине тогда, когда равновозможные исходы испытаний действительно имеют равные шансы на успех.
