Смешанным произведением векторов  называется скалярное произведение вектора
называется скалярное произведение вектора 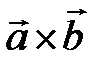 на вектор
на вектор 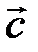 . Смешанное произведение обозначается
. Смешанное произведение обозначается  или
или 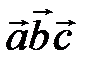 и представляет собой некоторое число.
и представляет собой некоторое число.
Выражение смешанного произведения через координаты.
Пусть заданы векторы 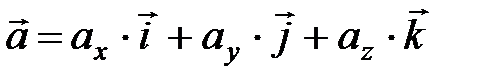 ,
,  ,
,  . Смешанное произведение векторов вычисляется по формуле
. Смешанное произведение векторов вычисляется по формуле  .
.
Некоторые приложения смешанного произведения.
1. Определение взаимной ориентации векторов в пространстве: если  , то
, то  - правая тройка, если
- правая тройка, если 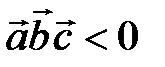 , то
, то  – левая тройка.
– левая тройка.
2. Установление компланарности векторов: векторы  компланарны тогда и только тогда, когда их смешанное произведение равно нулю (
компланарны тогда и только тогда, когда их смешанное произведение равно нулю (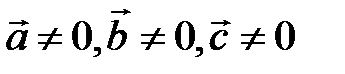 ).
).
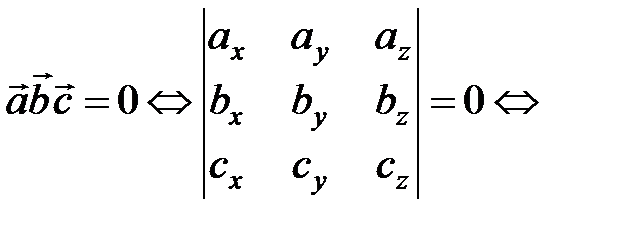 векторы
векторы  компланарны.
компланарны.
Объем параллелепипеда, построенного на векторах  вычисляется как
вычисляется как 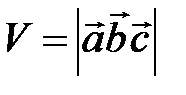 , а объем треугольной пирамиды, построенной на этих же векторах, равен
, а объем треугольной пирамиды, построенной на этих же векторах, равен  .
.
Пример. Вершинами пирамиды служат точки А(1;2;3), В(0;-1;1), С(2;5;2) и D(3;0;2). Найти объем пирамиды.
Решение. Находим векторы  .
.
 .
.
Находим  :
:
 .
.
Следовательно, 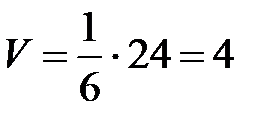 куб. ед.
куб. ед.
 2015-10-22
2015-10-22 671
671








