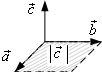
 Векторным произведением вектора
Векторным произведением вектора 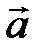 на вектор
на вектор 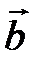 называется вектор
называется вектор 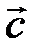 , который:
, который:
1) перпендикулярен векторам 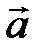 и
и 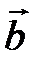 , т.е.
, т.е. 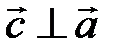 и
и 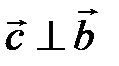 ;
;
2) имеет длину, численно равную произведению модулей векторов 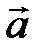 и
и 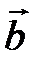 на синус угла между ними т.е.
на синус угла между ними т.е. 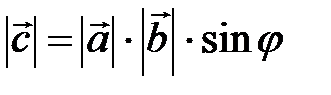 , где
, где 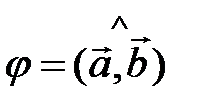 ;
;
3) векторы 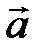 ,
, 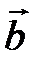 и
и 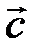 образуют правую тройку.
образуют правую тройку.
Векторное произведение обозначается 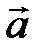 ×
× 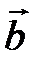 или
или 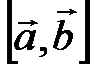 .
.
Из определения векторного произведения непосредственно вытекаеют следующие соотношения между ортами 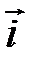 ,
,  и
и 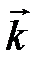 :
: 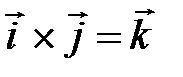 ,
, 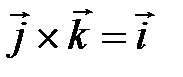 ,
, 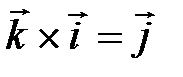 .
.
Свойства векторного произведения.
1. При перестановке сомножителей векторное произведение меняет знак, т.е. 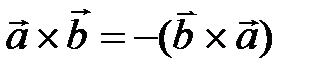 .
.
2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т.е. 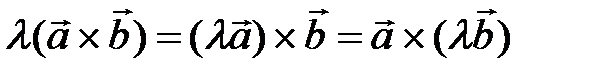 .
.
3. Два ненулевых вектора 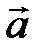 и
и 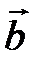 коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т.е.
коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т.е. 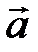 ||
|| 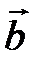
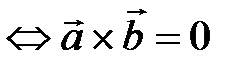 .
.
В частности 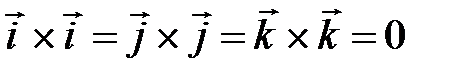 .
.
Векторное произведение обладает распределительным свойством:
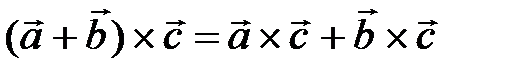 .
.
 2015-10-22
2015-10-22 499
499








