Скалярным произведением двух ненулевых векторов 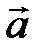 и
и 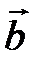 называется число, равное произведению длин этих векторов на косинус угла между ними.
называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначается 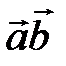 ,
, 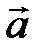 ∙
∙ 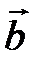 . Итак, по определению
. Итак, по определению 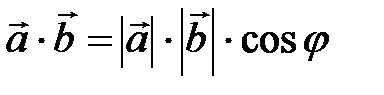 , где
, где 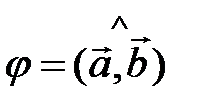 .
.
Свойства скалярного произведения.
1. Скалярное произведение обладает переместительным свойством: 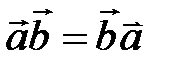 .
.
2. Скалярное произведение обладает сочетательным свойством относительно скалярного множителя: 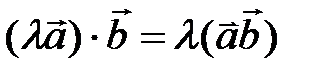 .
.
3. Скалярное произведение обладает распределительным свойством: 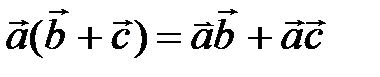 .
.
4. Скалярный квадрат вектора равен квадрату его длины: 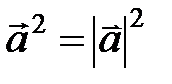 .
.
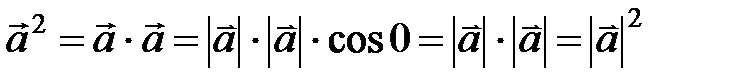 .
.
В частности: 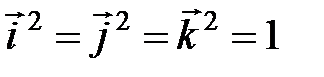 .
.
Если векторы 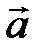 и
и 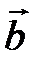 (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т.е. если
(ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т.е. если 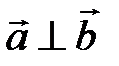 , то
, то 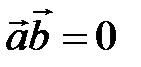 . Справедливо и обратное утверждение: если
. Справедливо и обратное утверждение: если 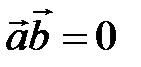 и
и 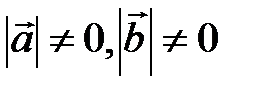 , то
, то 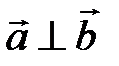 .
.
В частности: 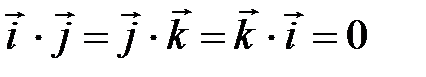 .
.
Скалярное произведение векторов равно сумме произведений их одноименных координат 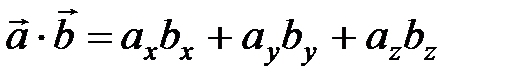 .
.
Некоторые приложения скалярного произведения
Угол между векторами
Определение угла φ между ненулевыми векторам 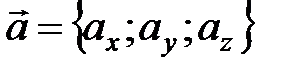 и
и 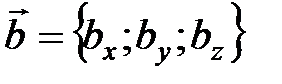 :
:
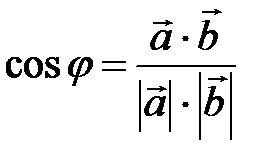 , т.е.
, т.е. 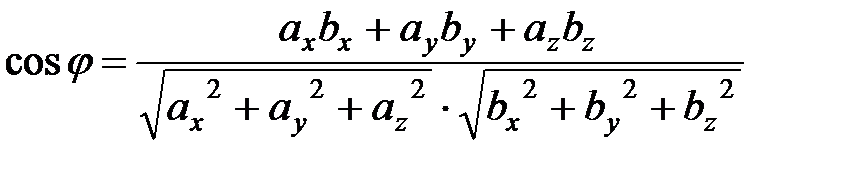 .
.
Отсюда следует условие перпендикулярности ненулевых векторов 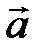 и
и 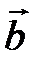 :
:
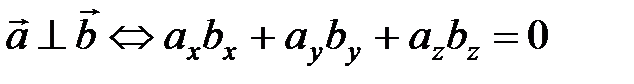 .
.
Работа постоянной силы
Пусть материальная точка перемещается прямолинейно из положения А в положение В под действием силы 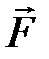 , образующей угол φ с перемещением
, образующей угол φ с перемещением 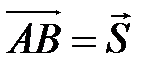 .
.
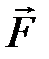
|
| φ |
| В |
| А |
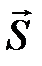
|
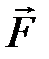 при перемещении
при перемещении 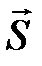 равна
равна 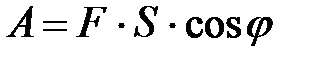 , т.е.
, т.е. 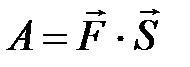 . Таким образом, работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения.
. Таким образом, работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения.
Пример 1. Вычислить работу, произведенную силой 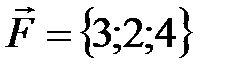 , если точка ее приложения перемещается прямолинейно из положения А(2;4;6) в положение В(4;2;7). Под каким углом к АВ направлена сила
, если точка ее приложения перемещается прямолинейно из положения А(2;4;6) в положение В(4;2;7). Под каким углом к АВ направлена сила 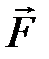 ?
?
Решение. Находим 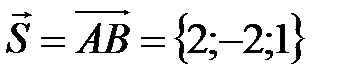 . Стало быть,
. Стало быть,
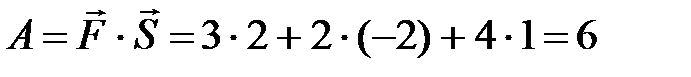 (ед. работы).
(ед. работы).
Угол φ между 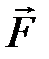 и
и 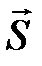 находим по формуле
находим по формуле 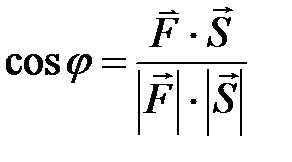 .
.
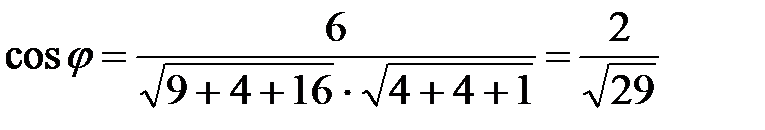 ,
, 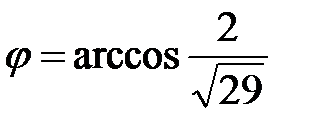 .
.
Пример 2. Векторы 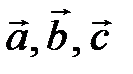 заданы в пространстве своими координатами.
заданы в пространстве своими координатами. 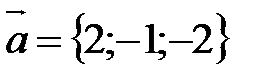 ,
, 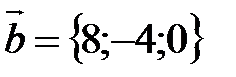 ,
, 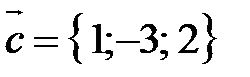 .
.
Найти: косинус угла между векторами 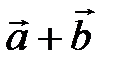 и
и 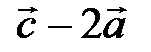 .
.
Решение.
Найдем векторы: 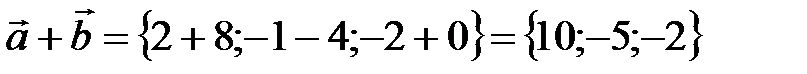 ,
,
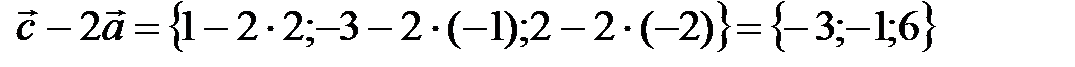 .
.
Найдем длины и скалярное произведение векторов:
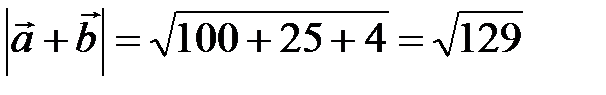 ,
,
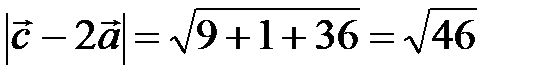 ,
,
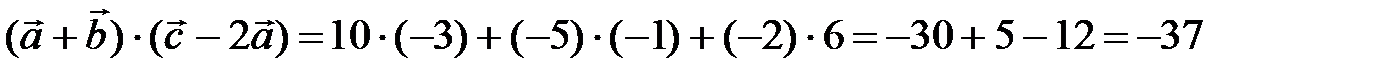 .
.
Косинус угла между полученными векторами находим по формуле
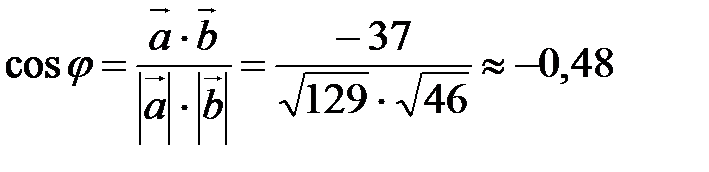 .
.
 2015-10-22
2015-10-22 564
564








