Число А называется пределом функции 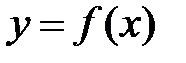 при
при 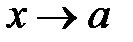 , если для любого положительного числа
, если для любого положительного числа 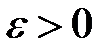 найдется такое положительное число
найдется такое положительное число 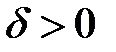 , что для всех
, что для всех 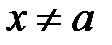 , удовлетворяющих неравенству
, удовлетворяющих неравенству 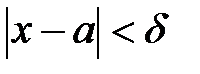 , выполняется неравенство
, выполняется неравенство 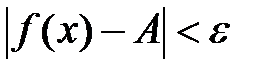 . Записывают
. Записывают 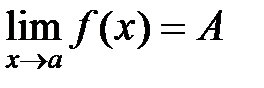 .
.
Аналогично:
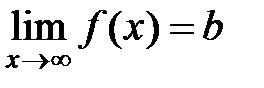 , если
, если 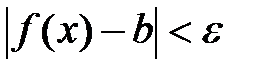 при
при 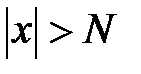 , N – произвольное положительное число.
, N – произвольное положительное число.
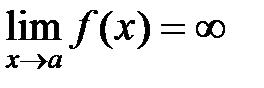 , если
, если 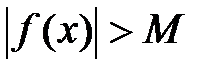 при
при 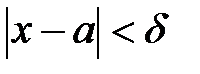 , где М – произвольное сколько угодно большое положительное число. В этом случае функция
, где М – произвольное сколько угодно большое положительное число. В этом случае функция 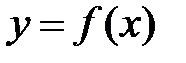 называется бесконечно большой величиной при
называется бесконечно большой величиной при 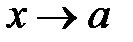 .
.
Если 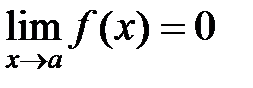 , то функция
, то функция 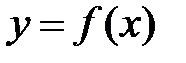 называется бесконечно малой величиной при
называется бесконечно малой величиной при 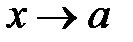 .
.
Простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A ≠ 0
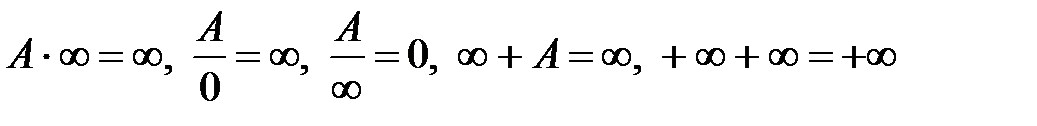 .
.
Практическое вычисление пределов основывается на следующих теоремах.
Если существуют конечные 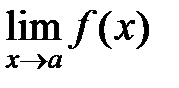 и
и 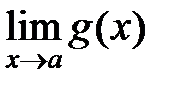 , то
, то
1) 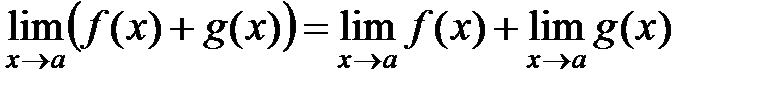
2) 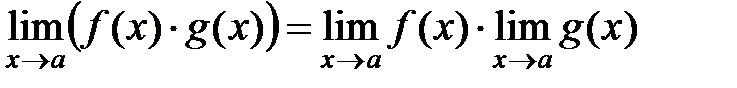
3) 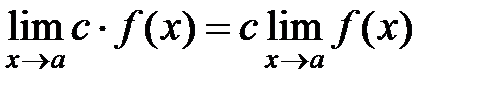 (с – константа)
(с – константа)
4) 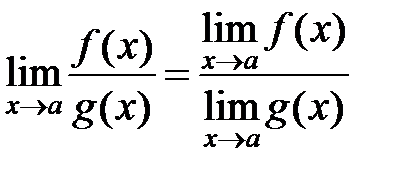 , (
, (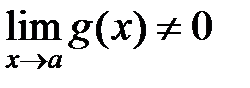 ).
).
Обычно для отыскания предела используют теоремы о пределах. Из этих теорем следует: если предельная точка входит в область определения функции, стоящей под знаком предела, то для его отыскания нужно найти значение функции в этой точке.
Пример 1.
а) 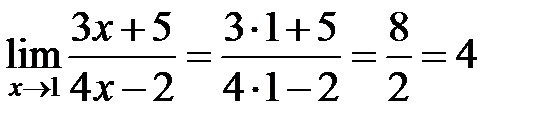 б)
б) 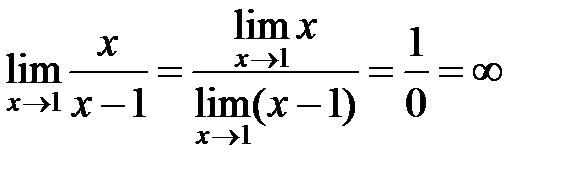
Но часто теоремы о пределах применить нельзя. Это бывает в случаях, так называемых неопределенных выражений: 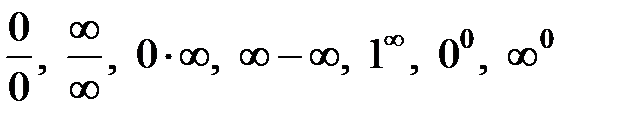 . Рассмотрим основные способы раскрытия неопределенностей.
. Рассмотрим основные способы раскрытия неопределенностей.
Пример 2. Найти предел 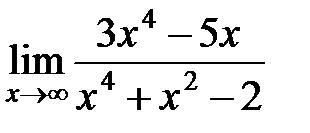
Решение. Теорему о пределе частного применять нельзя, т.к. числитель и знаменатель неограниченно возрастают при 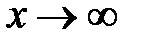 . Имеем неопределенность вида
. Имеем неопределенность вида 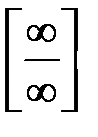 . В подобных примерах числитель и знаменатель дроби целесообразно разделить на высшую степень переменной. В нашем примере разделим числитель и знаменатель на
. В подобных примерах числитель и знаменатель дроби целесообразно разделить на высшую степень переменной. В нашем примере разделим числитель и знаменатель на 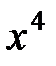 , затем перейдем к пределу.
, затем перейдем к пределу.
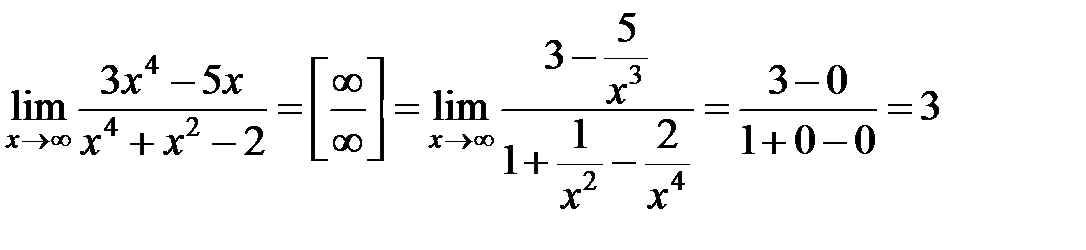
Пример 3. Найти предел 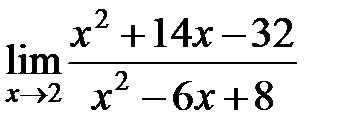
Решение. Подставляя х=2 в числитель и знаменатель дроби получим неопределенность вида 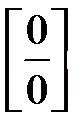 . В подобных примерах, когда числитель и знаменатель многочлены, их необходимо разложить на множители, после этого дробь сократить и прейти к пределу. Для разложения на множители квадратного трехчлена используем формулу
. В подобных примерах, когда числитель и знаменатель многочлены, их необходимо разложить на множители, после этого дробь сократить и прейти к пределу. Для разложения на множители квадратного трехчлена используем формулу 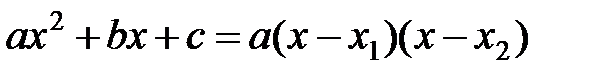 , где х1,х2 – корни соответствующего квадратного уравнения
, где х1,х2 – корни соответствующего квадратного уравнения
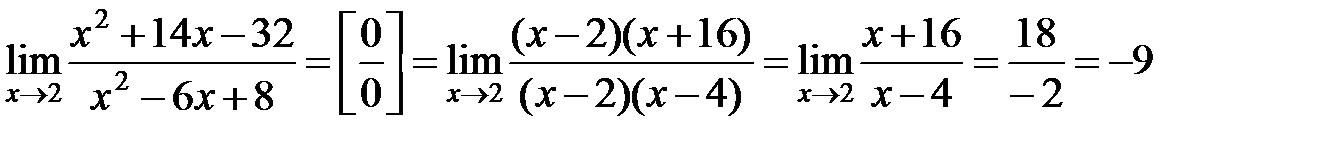 .
.
Пример 4. Найти предел 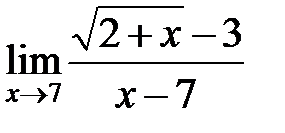
Решение. Если под знаком предела имеется иррациональность, то для раскрытия неопределенности 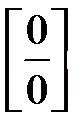 умножают числитель и знаменатель дроби на выражение сопряженное иррациональному, полученную дробь сокращают и переходят к пределу.
умножают числитель и знаменатель дроби на выражение сопряженное иррациональному, полученную дробь сокращают и переходят к пределу.
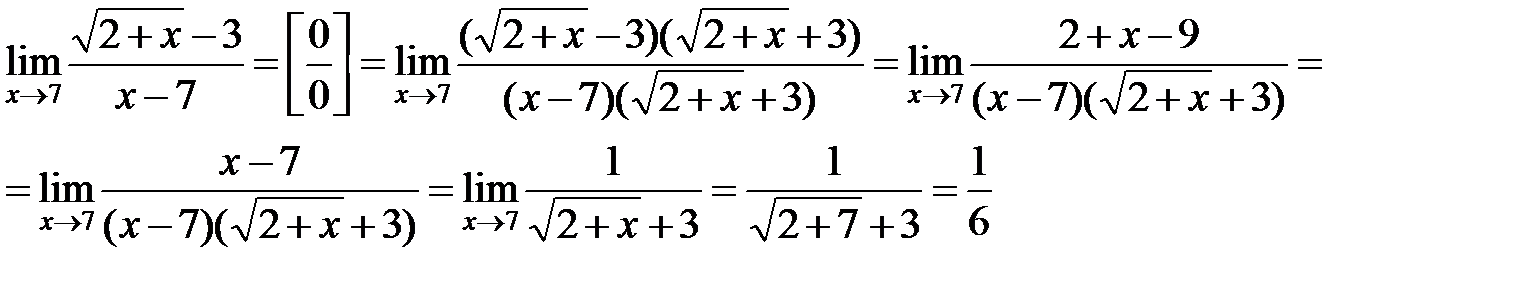
Пример 5. Найти предел 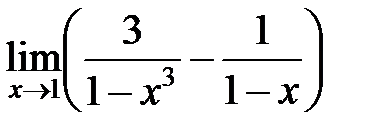
Решение. Преобразуем выражение, приведем дроби к общему знаменателю:
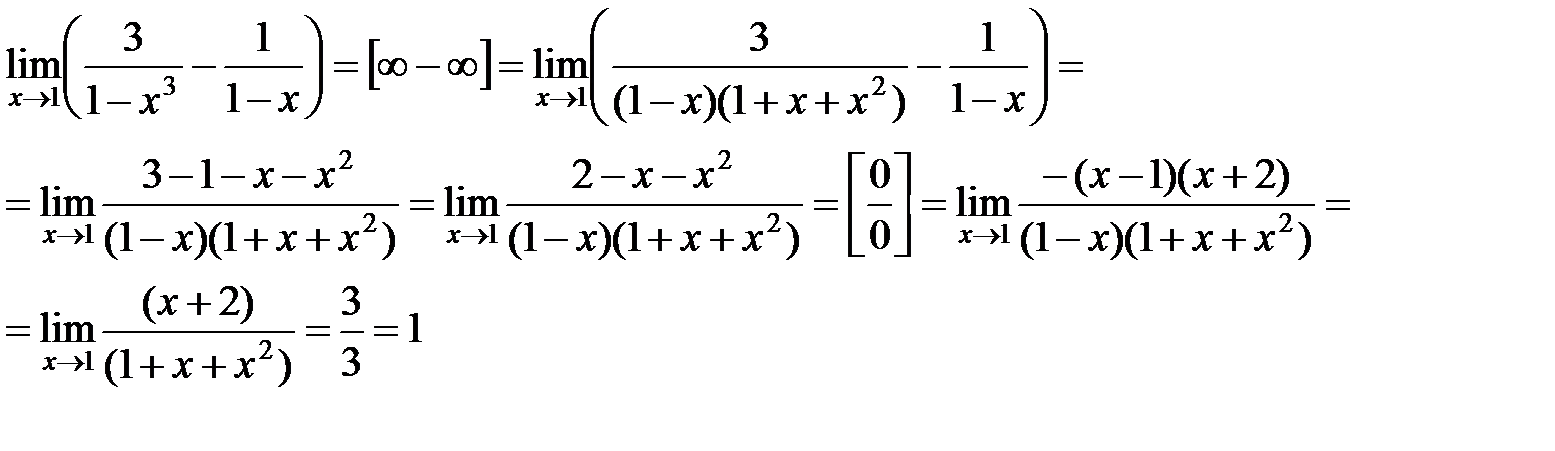
 2015-10-22
2015-10-22 343
343








