Пусть функция 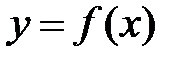 определена в точке
определена в точке 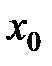 и в некоторой окрестности этой точки.
и в некоторой окрестности этой точки.
Функция 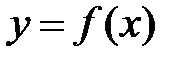 называется непрерывной в точке
называется непрерывной в точке 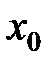 , если существует предел функции в этой точке и он равен значению функции в этой точке, т.е.
, если существует предел функции в этой точке и он равен значению функции в этой точке, т.е. 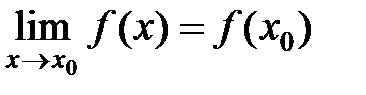 .
.
Это равенство означает выполнение трех условий:
1) Функция 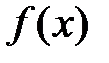 определена в точке
определена в точке 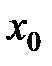 и в её окрестности;
и в её окрестности;
2) функция 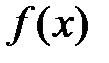 имеет предел при
имеет предел при 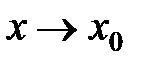 ;
;
3) предел функции в точке 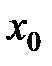 равен значению функции в этой точке.
равен значению функции в этой точке.
Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Если 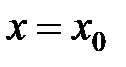 - точка разрыва функции
- точка разрыва функции 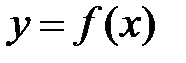 , то в ней не выполняется, по крайней мере, одно из условий первого определения непрерывности функции,
, то в ней не выполняется, по крайней мере, одно из условий первого определения непрерывности функции,
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Точка разрыва 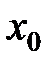 называется точкой разрыва первого рода функции
называется точкой разрыва первого рода функции 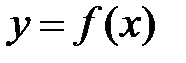 , если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е.
, если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е. 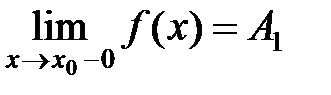 и
и 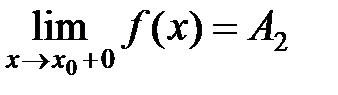 . При этом: а) если
. При этом: а) если 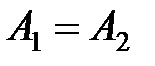 , то точка
, то точка 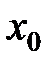 называется точкой устранимого разрыва;
называется точкой устранимого разрыва;
б) если 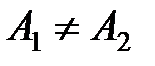 , то точка
, то точка 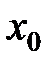 называется точкой конечного разрыва. Величину
называется точкой конечного разрыва. Величину 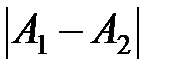 называют скачком функции в точке разрыва первого рода.
называют скачком функции в точке разрыва первого рода.
 Точка разрыва функции называется точкой разрыва второго рода, если, по крайней мере, один из односторонних пределов не существует или равен бесконечности.
Точка разрыва функции называется точкой разрыва второго рода, если, по крайней мере, один из односторонних пределов не существует или равен бесконечности.
Пример 1.
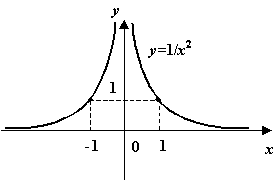
Функция 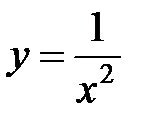 не определена в точке
не определена в точке 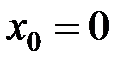 . Для функции
. Для функции 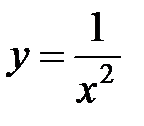
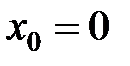 - точка разрыва второго рода.
- точка разрыва второго рода.
 Пример 2.
Пример 2.
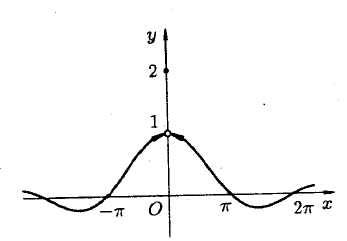
Для функции 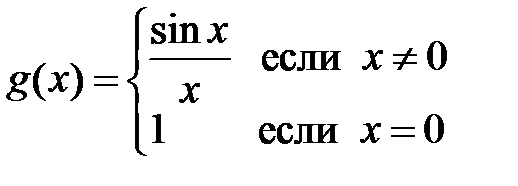 ,
, 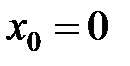 является точкой устранимого разрыва. Положив
является точкой устранимого разрыва. Положив 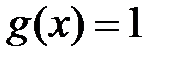 при
при 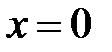 , разрыв устранится, функция станет непрерывной.
, разрыв устранится, функция станет непрерывной.
Пример 3.
Найти точки разрыва функции 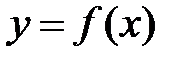 , если они существуют и построить график функции.
, если они существуют и построить график функции.
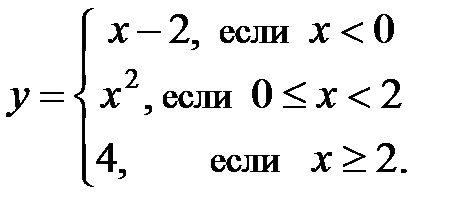
Данная функция задана несколькими аналитическими выражениями, каждое из которых представляет элементарную функцию. Поэтому, если данная функция имеет точки разрыва, то ими будут те точки, в которых она меняет аналитическое выражение, т.е х=0 и х=2. Исследуем эти точки. Найдем односторонние пределы в этих точках и значение функции.
х= 0
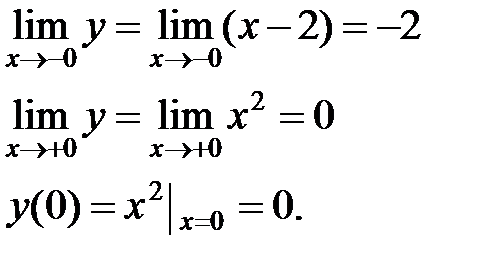
| x |
| -2 |
| y |
х= 2
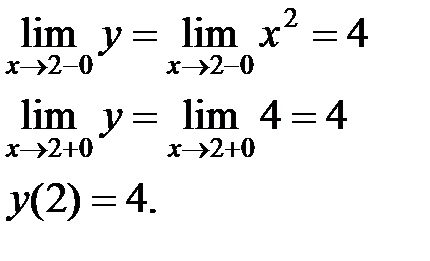
Все условия непрерывности в точке х=2 выполнены, функция в данной точке непрерывна.
Строим график данной функции (рис.6).
| Рисунок 6 |
Функция задается различными аналитическими выражениями для различных областей изменения независимой переменной. Требуется найти точки разрыва функции, если они существуют, построить график функции.
| 1. | 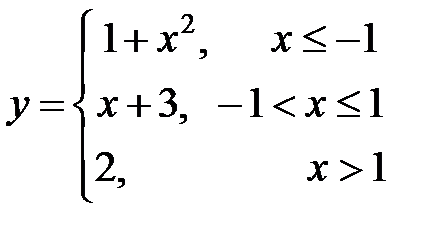 | 2. | 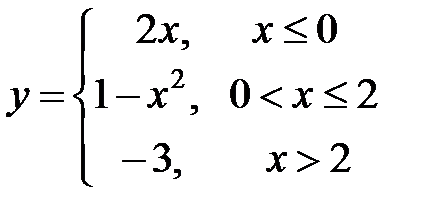 |
| 3. | 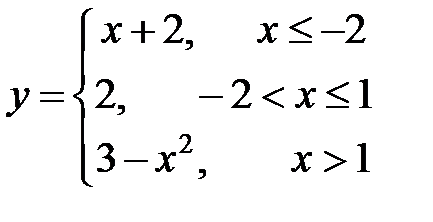 | 4. | 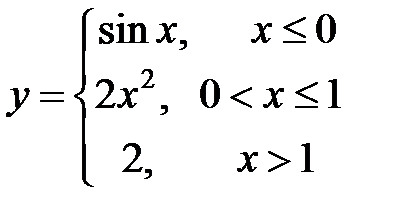 |
| 5. | 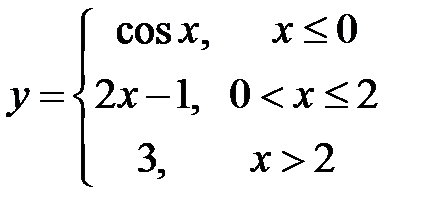 | 6. | 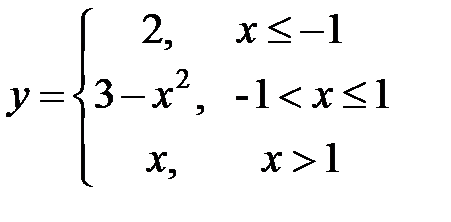 |
7. № 723-726, № 727, № 728 [1]
 2015-10-22
2015-10-22 841
841








