Правила дифференцирования:
1. 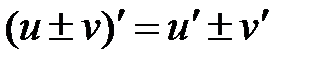
2. 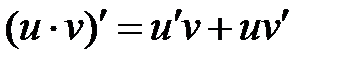 ;
; 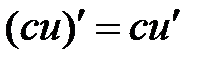 с-const
с-const
3. 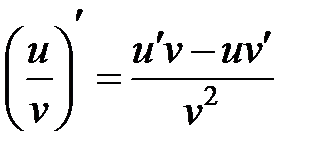 ;
; 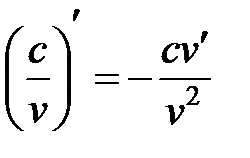 с-const
с-const
4. 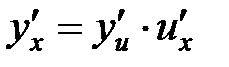 , если
, если 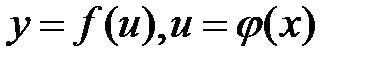 , т.е.
, т.е. 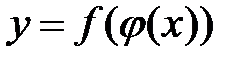
5. 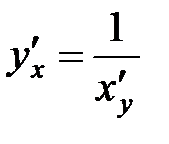 , если
, если 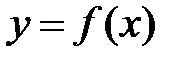 и
и 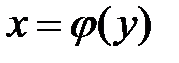 - взаимно обратные функции.
- взаимно обратные функции.
Формулы дифференцирования.
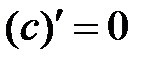
| ||
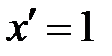
| ||
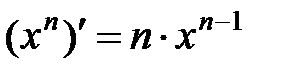 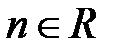
| 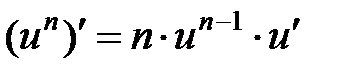 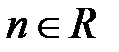
| |
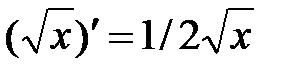
| 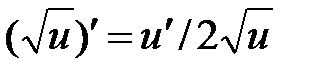
| |
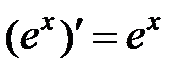
| 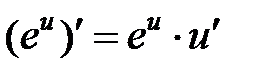
| |
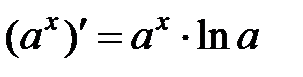
| 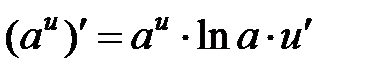
| |
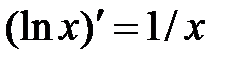
| 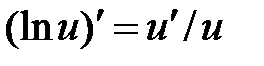
| |
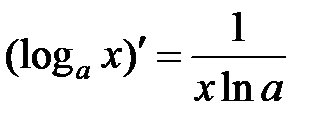
| 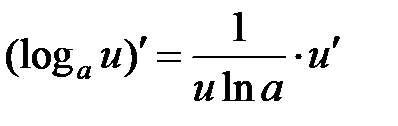
| |
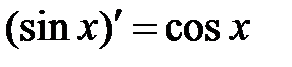
| 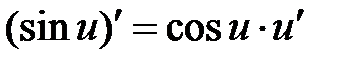
| |
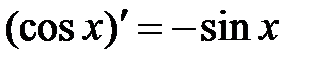
| 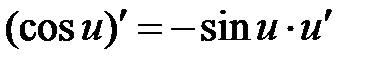
| |
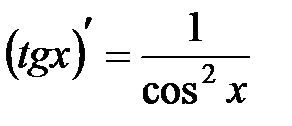
| 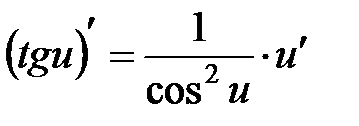
| |
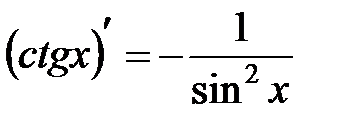
| 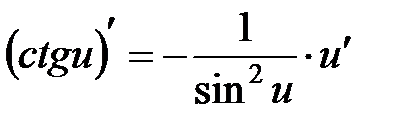
| |
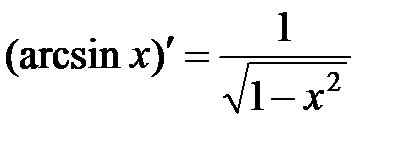
| 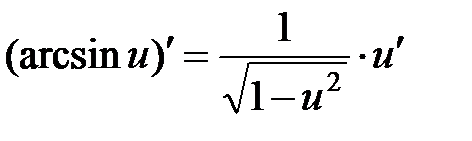
| |
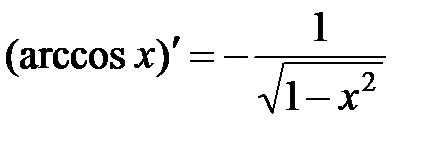
| 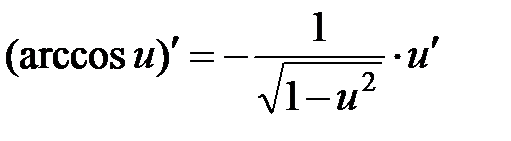
| |
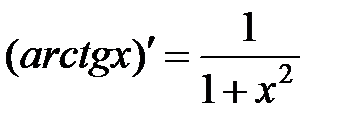
| 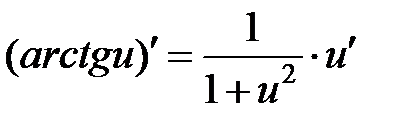
| |
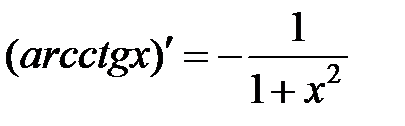
| 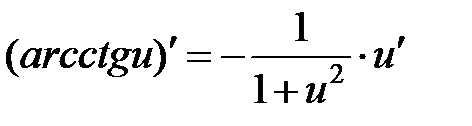
| |
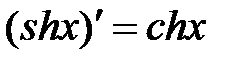
| 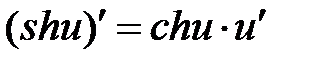
| |
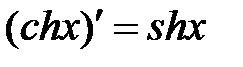
| 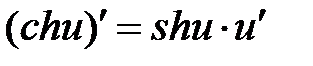
| |
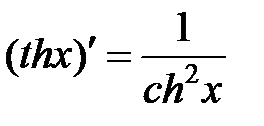
| 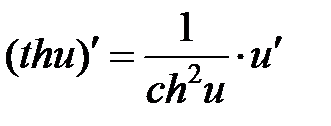
| |
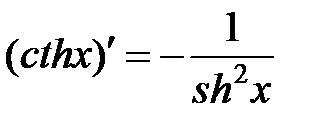
| 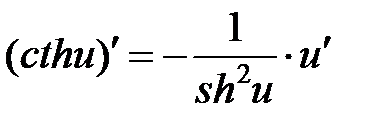
|
Примеры:
Пользуясь правилами и формулами дифференцирования, найти производные следующих функций:
1) 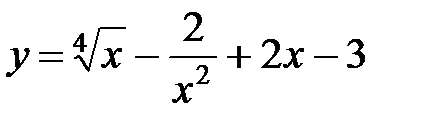
Перейдем к дробным показателям степени (выражения, содержащие корни) и к отрицательным показателям степени, получим выражение
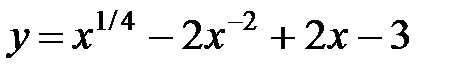
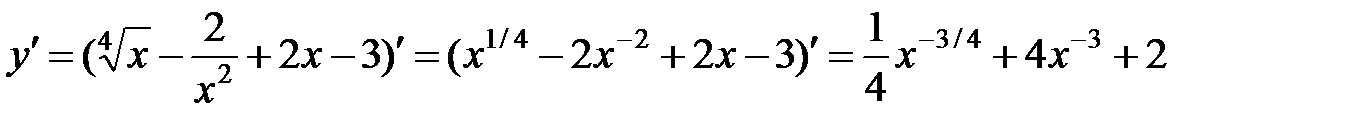
2) 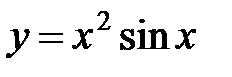 .
.
Воспользуемся формулой производной произведения 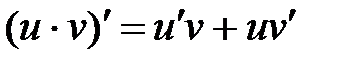

3) 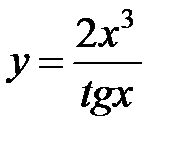 Воспользуемся формулой производной частного
Воспользуемся формулой производной частного 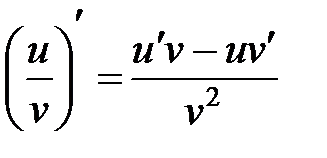
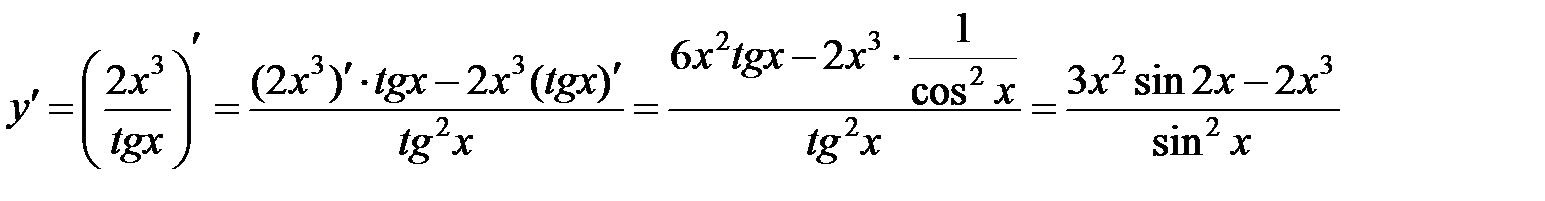
Задания для самостоятельной работы
Найти производные
1. 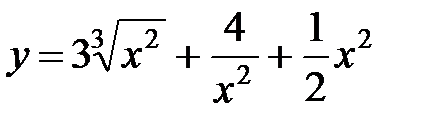 6.
6. 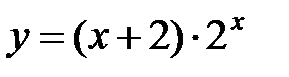
2. 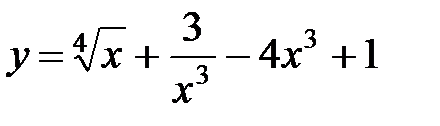 7.
7. 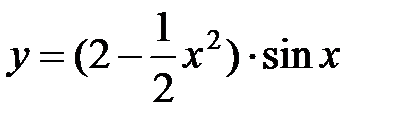
3. 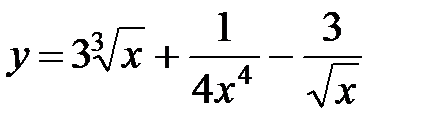 8.
8. 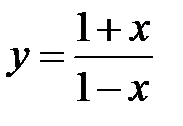
4. 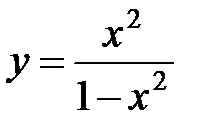 9.
9. 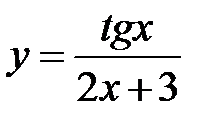
5. 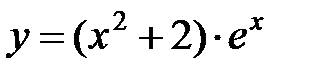 10.
10. 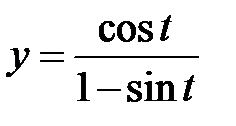
11. № 745-750, № 771-777 [1]
12. № 778 -780, № 782,№ 783 [1]
Рекомендуемая литература: [2] стр. 68-96, [7] стр. 167-177, [4] стр. 186-201.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 14
Тема: Нахождение производных сложных функций. Логарифмическое дифференцирование.
 2015-10-22
2015-10-22 323
323








