Производная 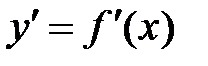 функции
функции 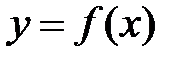 так же является функцией и называется производной первого порядка.
так же является функцией и называется производной первого порядка.
Если функция 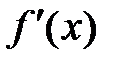 дифференцируема, то ее производная называется производной второго порядка и обозначается
дифференцируема, то ее производная называется производной второго порядка и обозначается 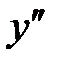 (или
(или 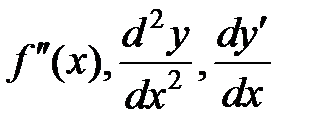 ).
).
Таким образом, 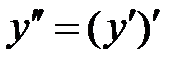 .
.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается 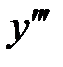 .
.
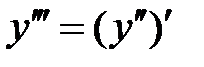 ,
, 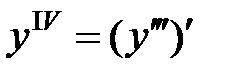 …
…
Производной n –го порядка (или n –й производной) называется производная от производной порядка (n-1): 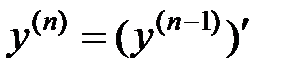 .
.
Производные порядка выше первого называются производными высших порядков.
Пример 1. 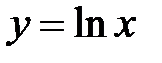 , найти производную третьего порядка.
, найти производную третьего порядка.
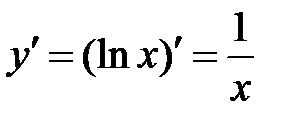 ;
;
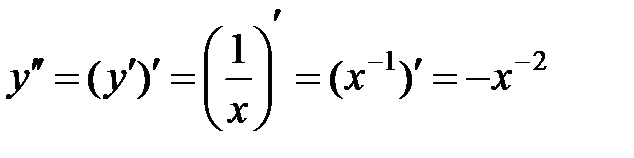 ;
;
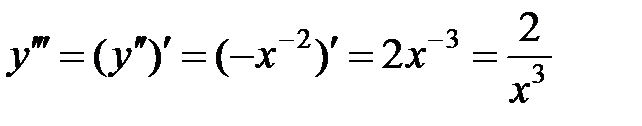 .
.
Пример 2. Найти 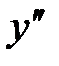 , если
, если 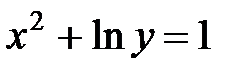 .
.
Дифференцируем уравнение по х: 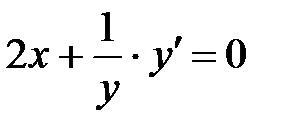 .Отсюда находим
.Отсюда находим 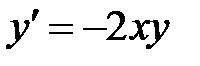 . Далее
. Далее 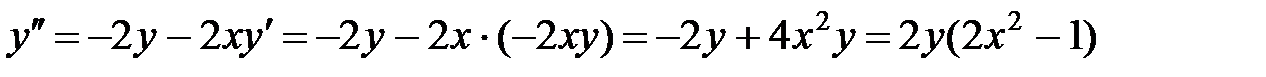 .
.
Пример 3. Найти вторую производную, если 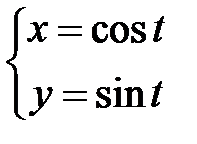 .
.
Функция задана параметрическими уравнениями. Вторую производную находим по формуле 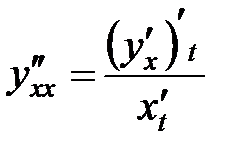 .
.
Решение: Находим первую производную 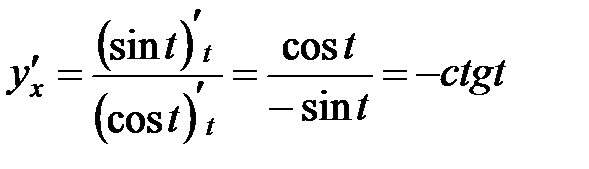 .
.
Находим вторую производную 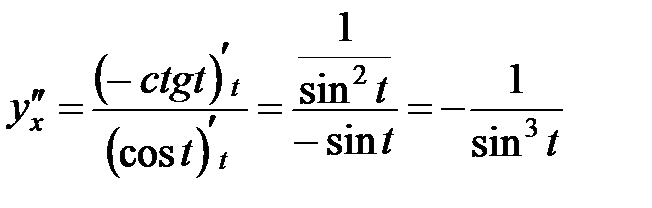 .
.
 2015-10-22
2015-10-22 307
307








