2015-10-22
324
Если кривая задана уравнением 
, то производная 
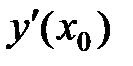численно равна угловому коэффициенту касательной к этой кривой в точке с абсциссой 
: 
. Чтобы составить уравнение касательной, используем уравнение прямой в виде 
. Получим: 
- уравнение касательной.
Нормалью к кривой называется прямая, перпендикулярная касательной и проходящая через точку касания. Угловой коэффициент нормали 
. Уравнение нормали имеет вид 
.
Пример 1.
Составить уравнения касательной и нормали к графику функции 
в точке с абсциссой 
.
Решение: Из уравнения кривой определим ординату точки касания 
; 
.
Из этого же уравнения найдем производную и значение производной в точке : 
, 
.
Составим уравнение касательной: 
или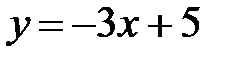 
.
Составим уравнение нормали: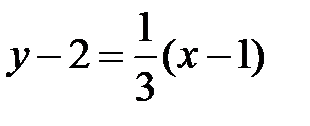 
или 
.
