Наибольшее и наименьшее значения функции на отрезке

Пусть функция 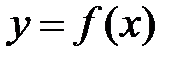непрерывна на отрезке 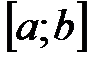. Функция достигает своего наибольшего и наименьшего значения либо во внутренней точке отрезка 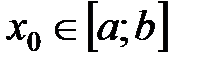, либо на границе х₀=а или х₀=b. Если 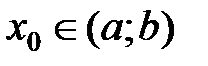, то х₀ - критическая точка данной функции.

Алгоритм нахождения наибольшего и наименьшего значения функции на отрезке:

1. Найти критические точки функции, т.е. решить уравнение .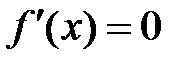

2. Вычислить значение функции в тех критических точках, которые принадлежат интервалу .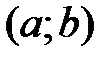

3. Вычислить значение функции на концах отрезка в точках х=а и х=b.

4. Среди всех полученных значений функции выбрать наибольшее и наименьшее.

Если функция 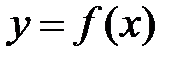на отрезке 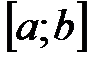не имеет критических точек, то это означает, что на нем функция монотонна убывает или возрастает. Следовательно, наибольшее и наименьшее значение принимает только на концах отрезка.

Пример. Найти наибольшее и наименьшее значение функции 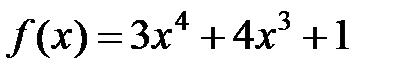на отрезке [-2 ;1 ].

1.

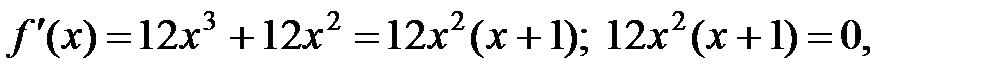
х₁ =0, х ₂=-1, обе точки принадлежат данному отрезку;

2. f (0)=1; f (-1)=3-4+1=0;

3. f (-2)=48-32+1=17; f (1)=3+4+1=8.

4. Наименьшее значение функции на отрезке [-2 ;1 ] f (-1)= 0,

наибольшее значение функции на отрезке [-2 ;1 ] f (-2)=17.