Функция  называется возрастающей в интервале
называется возрастающей в интервале  , если для любых двух точек
, если для любых двух точек  и
и  из указанного интервала, удовлетворяющих неравенству
из указанного интервала, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  , если
, если  , функция называется неубывающей.
, функция называется неубывающей.
Иными словами – значения возрастающей функции увеличиваются одновременно со значением аргумента.
Функция  называется убывающей в интервале
называется убывающей в интервале  , если для любых двух точек
, если для любых двух точек  и
и  из указанного интервала, удовлетворяющих неравенству
из указанного интервала, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  , если
, если  , функция называется невозрастающей.
, функция называется невозрастающей.
Признаки монотонности функции:
- если функция  дифференцируема на интервале
дифференцируема на интервале  и
и  во всех точках интервала, то функция
во всех точках интервала, то функция  возрастает на этом интервале;
возрастает на этом интервале;
- если функция  дифференцируема на интервале
дифференцируема на интервале  и
и  во всех точках интервала, то функция
во всех точках интервала, то функция  убывает на этом интервале.
убывает на этом интервале.
Пример. Исследовать функцию  на возрастание, убывание.
на возрастание, убывание.

 на интервалах
на интервалах  , следовательно, на этом промежутке функция возрастает (знак производной «+»).
, следовательно, на этом промежутке функция возрастает (знак производной «+»).
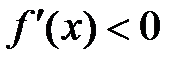 на интервале (-1;1), следовательно, функция здесь убывает (знак производной «–»).
на интервале (-1;1), следовательно, функция здесь убывает (знак производной «–»).
Экстремумы функции.
Точка  называется точкой максимума функции
называется точкой максимума функции  , если значение
, если значение  является наибольшим в некоторой окрестности этой точки.
является наибольшим в некоторой окрестности этой точки.
Точка 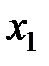 называется точкой минимума функции
называется точкой минимума функции  , если значение
, если значение  является наименьшим в некоторой окрестности этой точки.
является наименьшим в некоторой окрестности этой точки.
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках – экстремумами функции.
Если  - точка экстремума для функции
- точка экстремума для функции  , то в этой точке производная функции либо равна нулю
, то в этой точке производная функции либо равна нулю  , либо не существует.
, либо не существует.
Если при переходе (слева направо) через критическую точку  производная
производная  меняет знак с (+) на (-), то точка
меняет знак с (+) на (-), то точка  является точкой максимума; если с (-) на (+), то точкой минимума; если знака не меняет, то экстремума нет.
является точкой максимума; если с (-) на (+), то точкой минимума; если знака не меняет, то экстремума нет.
Правило исследования функции на экстремум:
1) Найти критические точки функции 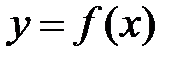 . Для этого решить уравнение
. Для этого решить уравнение 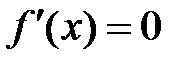 ;
;
2) Выбрать из них лишь те точки, которые являются внутренними точками области определения функции;
3) Исследовать знак производной слева и справа от каждой из выбранных точек;
4) Вычислить значение функции в выбранных точках.
Пример. Найти экстремум функции  .
.
1) Область определения функции: 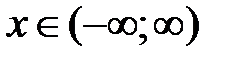 ;
;
2)  , производная равна нулю в точке х =8 и не существует в точке х =0. Критические точки х =0 и х =8.
, производная равна нулю в точке х =8 и не существует в точке х =0. Критические точки х =0 и х =8.
3) Определяем знак производной в интервалах  .
.
| + |
| + |
| 8 |
| ─ |
Точка х= 0 – точка максимума, точка х =8 – точка минимума.  ,
,  .
.
 2015-10-22
2015-10-22 247
247








