Лабораторна робота 10

Розв’язання диференційних рівнянь в частинних похідних

Теоретичні відомості

Диференційним рівнянням в частинних похідних називається рівняння відносно функції декількох змінних (обов'язково більш ніж однієї), що містить саму цю функцію (необов'язково) і її частинні похідні за різними аргументами.

Лінійне рівняння в частинних похідних другого порядку має вигляд:

.

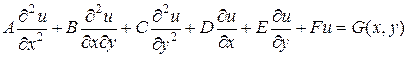Рівняння є еліптичного типу, якщо 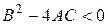, параболічного типу, якщо 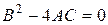, гіперболічного типу, якщо .

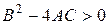Розв’язком рівняння є функція .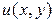

Чисельне вирішення диференціальних рівнянь в частинних похідних методом кінцевих різниць полягає в наступному:

1. Побудова в заданій області сітки з (n–1)(m–1) вузлів (точкиперетину ліній сітки). Для розв’язання рівняння необхідно визначити наближені значення шуканої функції u _i,j у вузлах сітки (i=1, 2…n–1, j=1, 2, …m–1).

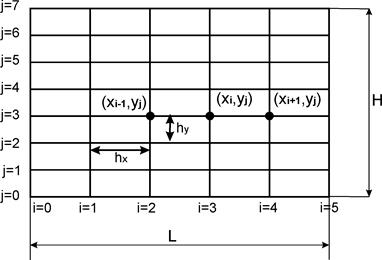
Побудова сітки в прямокутній області при n=5, m=7

2. Наведення похідних у формі кінцевих різниць:

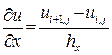
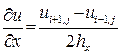(10.1)

або

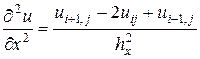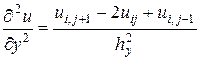, (10.2)

де ,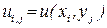

, ,

,

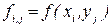
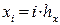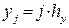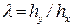
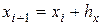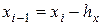
3. Складання різницевого рівняння для кожного внутрішнього вузла.

4. Перетворення початкових і граничних умов до дискретного вигляду.

5. Розв’язання отриманої системи алгебраїчних рівнянь.

Постановка задачі для рівняння теплопровідності. Відшукати функцію u(x,t), яка в області задовольняє рівнянню:

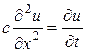(10.3)

початковій умові:

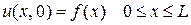(10.4)

і граничним умовам:

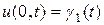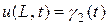, (10.5)

Явна схема. Використовуючи формули (10.1), (10.2), перейдемо від рівняння в частинних похідних (10.3) до різницевого рівняння:

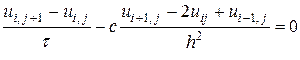, i=1, 2,…n–1, j=1, 2,…m–1.

Після перетворень отримаємо:

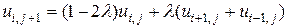, i=1, 2,…n-1, j=1, 2,…m-1. (10.6)

Формула (10.6) представляє явну систему рівнянь для невідомих u_i,j+1. Перший рядок рішення (j=0) знаходять на підставі початкових і граничних умов. Другий рядок можна обчислити безпосередньо з (10.6), поклавши j=0. Таким же чином можна обчислити третій рядок, поклавши j=1. Далі рішення обчислюється аналогічним чином.

Процес обчислення рішення збігається і стійкий, якщо:

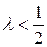або 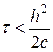. (10.7)

Неявна схема для рівняння теплопровідності:

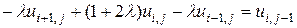, i=1, 2,…n-1, j=1, 2,…m-1. (10.8)

Схема (10.8) збігається і стійка для всіх l>0. Тому можна брати достатньо велику величину кроку за часом.

Приклад 10.1. Розв’язати одновимірне рівняння теплопровідності 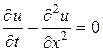явним методом для 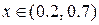, , 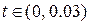h=0.1, t=0.005.

Початкова умова: .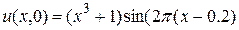

Крайові умови: .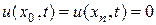

Визначимо сітку: , .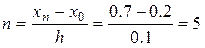

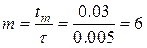Умова збіжності виконується, оскільки .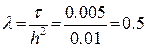

Підставивши в (10.6) значення ,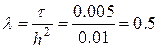

отримаємо розрахункову формулу

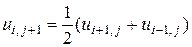i=1, 2, …, n-1, j=1, 2, …, 5.

Початкова умова 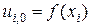, де

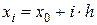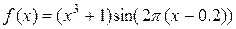, , i= 1, 2, 3, 4.

Крайові умови: 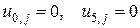, j=0,1, 2, …, 6.

За допомогою початкової умови обчислюємо перший рядок розв’язку (j=0, i= 1, 2, 3, 4). Наприклад,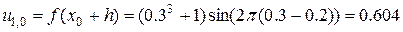

Далі обчислюємо другий рядок розв’язку (j=1).

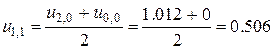
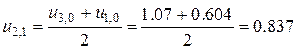
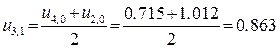
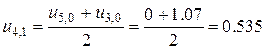
В таблиці наведені розраховані значення температури у вузлах сітки

	i
j	xi tj	0.2	0.3	0.4	0.5	0.6	0.7
			0.604	1.012	1.07	0.715
	0.005		0.506	0.837	0.863	0.535
	0.010		0.418	0.685	0.686	0.432
	0.015		0.342	0.552	0.558	0.343
	0.020		0.276	0.45	0.448	0.279
	0.025		0.225	0.362	0.365	0.224
	0.03		0.181	0.295	0.293	0.182

Для розв’язання рівнянь параболічного типу призначена функція pdesolve, яка застосовується в рамках обчислювального блоку. Блок розв’язку починається зі слова Given. Рівняння, які необхідно вирішити, повинні бути визначені усередині обчислювального блоку.

pdesolve (u, x, xrange, t, trange, [xpts], [tpts]) – повертає скалярну (для єдиного початкового рівняння) або векторну (для системи рівнянь) функцію двох аргументів (x,t), що є розв’язком диференціального рівняння (або системи рівнянь) в частинних похідних.

u – ім'я функції або вектор імен функцій (без вказівки імен аргументів). Ці функції, а також граничні умови (у формі Дирихле або Неймана) повинні бути визначені перед застосуванням функції pdesolve в обчислювальному блоці після ключового слова Given. Якщо вирішується не система рівнянь в частинних похідних, а єдине рівняння, то, відповідно, вектор u повинен містити тільки одне ім'я функції і перетворюється на скаляр;

х – просторова координата (ім'я аргументу невідомої функції);

xrange – просторовий інтервал. Цей вектор повинен складатися з двох дійсних чисел, що представляють ліву і праву межу розрахункового інтервалу;

t – час;

trange – часовий інтервал. Вектор складається з двох дійсних чисел, що представляють ліву і праву межу розрахункового інтервалу за часом;

xpts – кількість просторових точок дискретизації (може не указуватися явно, у такому разі буде підібрано програмою автоматично);

tpts – кількість шарів, тобто інтервалів дискретизації за часом (також може не указуватися явно).

Примітки:

1. При записі рівнянь усередині обчислювального блоку після імені функції в дужках указують її аргументи, наприклад u(x,t). Для позначення похідних використовується нижні індекси (клавіша «.»). Наприклад, u_xx(x,t) – друга похідна по х.

2. Для розв’язання рівняння необхідно задати початкові умови і n граничних умов (n – порядок диференціального рівняння).

Завдання

1. Розв’язати явним методом рівняння теплопровідності (10.3) з постійними коефіцієнтами на сітці з 10 вузлів по х (i=0, 1, … 10) з кроком 0.1. Виконати розрахунки для 10 шарів за часом (j=0, 1, … 10) з кроком 0,005, , , , .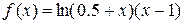

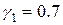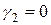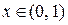2. Розв’язати рівняння теплопровідності за допомогою вбудованої функції pdesolve

Порядок виконання

Розв’язання за явною схемою

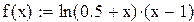
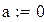
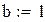
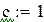
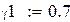
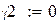
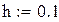
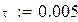
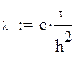
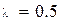
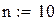
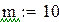
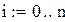
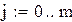
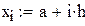
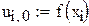– початкові умови

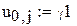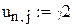, – граничні умови

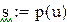
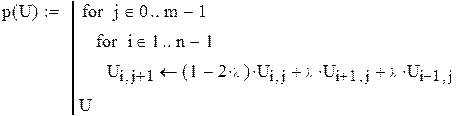
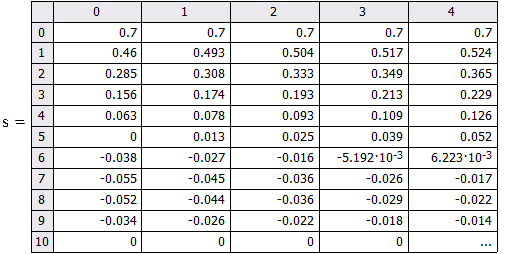
Таблиця значень функції у вузлах сітки

Графічне наведення розв’язку для 0, 4, 8-го шарів за часом

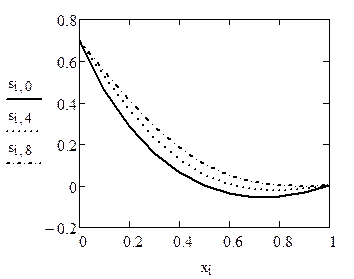Розв’язання за допомогою вбудованої функції pdesolve

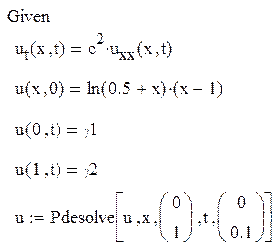
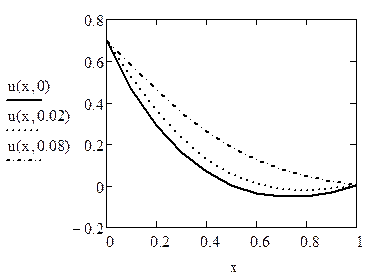Контрольні питання

1. Які рівняння називаються диференціальними рівняннями в частинних похідних?

2. Класифікація рівнянь в частинних похідних.

3. Які фізичні задачі приводять до рівняння: а) параболічного; б) гіперболічного; в) еліптичного типу.

4. Що включає постановка задачі розв’язання диференціального рівняння в частинних похідних?

5. Що таке задача Коші, крайова задача, змішана задача?

6. У чому полягає суть методу кінцевих різниць?

7. Етапи розв’язання диференціального рівняння методом кінцевих різниць.

8. Що таке збіжність і стійкість різницевої схеми?

9. Яка схема називається явною, неявною?

10. Чи можна використати явну схему для розв’язання параболічного рівняння, якщо крок за координатою дорівнює 0,1, та крок за часом t=0,01? Обґрунтувати відповідь.

11. Як розв’язати параболічне рівняння за допомогою функції pdesolve?

12. У якому вигляді повертає результат функція pdesolve?

Варіанти завдань

Варіант	f(x)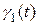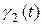
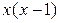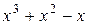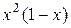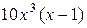		0,5
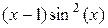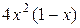			0.5
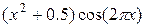		0.5	1.5
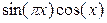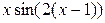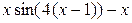			–1
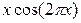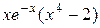			–0.4
	arctg(x)		p/4
	1+x2
	1/(1+x)		0.5
	ln(1+x)		ln2
	e-x		1/e
	(x2+0.5)cos(px)	0.5	–1.5
	x2+x+1
	cos(x)		cos1
	xsin(x-1)
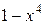	1/(1+x2)		0.5
	xe-x		1/e
	1-x2

СПИСОК ЛІТЕРАТУРИ

1. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. – М.: Высш. шк., 1994. – 544 с.

2. Ракитин В.И. Руководство по методам вычислений и приложения Mathcad. – М.: ФИЗМАТЛИТ, 2005. – 264 с.

3. Кирьянов Д.В. Самоучитель MathCAD 11. – С.Пб.: БХВ-Петербург, 2003.– 560 с.

4. Волков Е.А. Численные методы: Уч. пособие для вузов. – М.: Наука, 1987. – 248 с.

5. Брановицкая С.В., Медведев Р.Б., Фиалков Ю.Я. Вычислительная математика в химии и химической технологии. – К.: Вища шк., 1986.– 216 с.

6. Плис А.И., Сливина Н.А. MathCAD: математический практикум для экономистов и инженеров. – М.: Финансы и статистика, 1999. – 655 с.

7. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Наука, 1987– 632 с.

8. Амосова О.А., Григорьев В.П., Зайцева С.Б. Вычислительные методы с применением математического пакета Mathcad: Лабораторный практикум (http://www.exponenta.ru/educat/systemat/amosova/lr.asp).