Метод письменной замены переменной (подстановки)

План

1. Вводим новую переменную (подстановку)

2. Дифференцируем подстановку.

3. Вводим новую переменную в подынтегральное выражение.

4. Вычисляем интеграл.

5. Возвращаемся к старой переменной.

Примеры (см. задание 1а):

1)

.

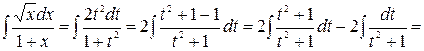
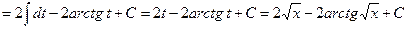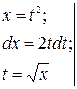
2)

.

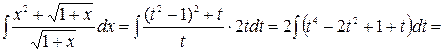
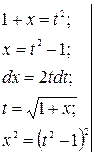
3) .

Метод интегрирования по частям

Этот метод применяют для интегралов вида:

а) , , ;

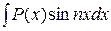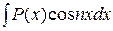б) , , , , ;

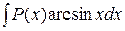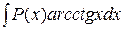в) , ;

где 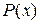- многочлен.

Формула интегрирования по частям имеет вид:

.

1) Для интегралов типа а) принимают U =P(x), все остальное равно dV.

2) Для интегралов типа б) принимают dV =P(x)dx.

3) для интегралов типа в) за U принимают любую функцию, метод применяют дважды.

Примеры (см. задание 1б):

1) ;

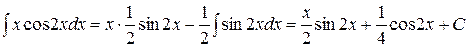2)

;

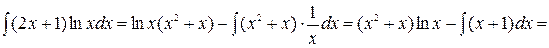
3)

.

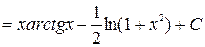4) можно решение записать иначе:

Получили первоначальный интеграл, обозначим его за y

;

;

+С.