1) 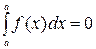 ; 2)
; 2) 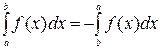 ;
;
3) 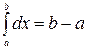 ; 4)
; 4) 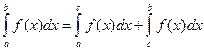 ;
;
5) 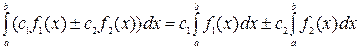 ;
;
6) Если 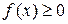 , то
, то 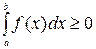 ;
;
Если 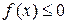 , то
, то 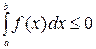 .
.
Следствие. Если 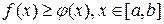 , то
, то 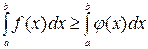 .
.
7) Если f(x) непрерывна на [ a, b ], m, M - ее соответственно наименьшее и наибольшее значение на [ a, b ], то справедлива оценка
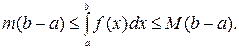
8) (Теорема о среднем). Если f(x) непрерывна на [ a, b ], то существует хотя бы одна точка 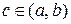 такая, что
такая, что
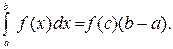
Формула Ньютона-Лейбница
Пусть f(x) – непрерывна на [ a, b ], F(x) – первообразная функции f(x) на [ a,b ], тогда определенный интеграл равен приращению первообразной (т.е. неопределенного интеграла) на этом отрезке:
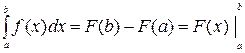
Примеры
1) 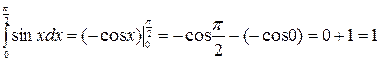 ;
;
2) 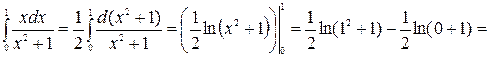
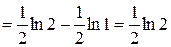
Интегрирование по частям
(см. интегрирование по частям в разделе "Неопределенный интеграл")
Формула интегрирования по частям для определенного интеграла имеет вид
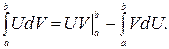
Пример.
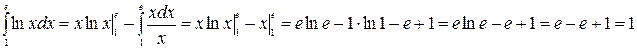
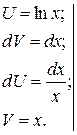
 2015-10-22
2015-10-22 264
264








