1) Находим первые два приближения по формулам:
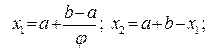 , где
, где 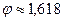 - пропорция «золотого сечения».
- пропорция «золотого сечения».
Для отрезка 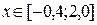 имеем
имеем
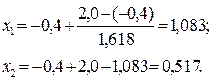
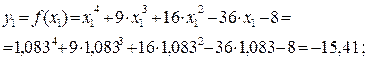
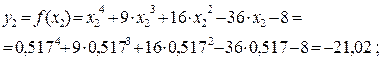
Так как 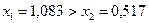 и
и 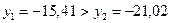 , то правый отрезок
, то правый отрезок 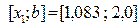 отбрасываем и считаем, что
отбрасываем и считаем, что 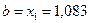 , а
, а 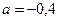 не меняется.
не меняется.
Так как 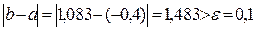 , то нужно выполнить следующее приближение.
, то нужно выполнить следующее приближение.
2) Теперь по правилу «золотого сечения» делим отрезок 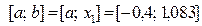 , причем точка
, причем точка 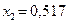 уже находится внутри этого отрезка, а точку
уже находится внутри этого отрезка, а точку 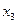 ищем как точку, симметричную точке
ищем как точку, симметричную точке 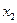 относительно середины отрезка
относительно середины отрезка 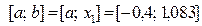 , т.е. по формуле
, т.е. по формуле
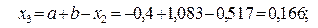
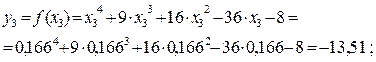
Так как 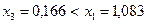 , а
, а 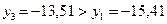 , то левый отрезок
, то левый отрезок 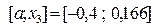 отбрасываем и считаем, что
отбрасываем и считаем, что 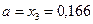 , а
, а 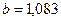 не меняется.
не меняется.
Так как 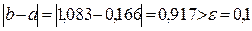 , то нужно выполнить следующее приближение.
, то нужно выполнить следующее приближение.
3) Теперь по правилу «золотого сечения» делим отрезок 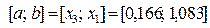 , причем точка
, причем точка 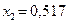 уже находится внутри этого отрезка, а точку
уже находится внутри этого отрезка, а точку 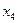 ищем как точку, симметричную точке
ищем как точку, симметричную точке 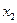 относительно середины отрезка
относительно середины отрезка 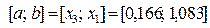 , т.е. по формуле
, т.е. по формуле
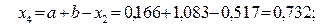
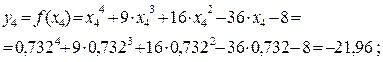
Так как 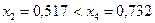 , а
, а 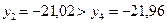 , то левый отрезок
, то левый отрезок 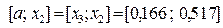 отбрасываем и считаем, что
отбрасываем и считаем, что 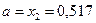 , а
, а 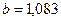 не меняется.
не меняется.
Так как 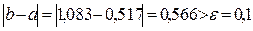 , то нужно выполнить следующее приближение.
, то нужно выполнить следующее приближение.
4) Теперь по правилу «золотого сечения» делим отрезок 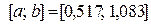 , причем точка
, причем точка 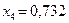 уже находится внутри этого отрезка, а точку
уже находится внутри этого отрезка, а точку 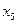 ищем как точку, симметричную точке
ищем как точку, симметричную точке 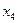 относительно середины отрезка
относительно середины отрезка 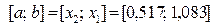 , т.е. по формуле
, т.е. по формуле
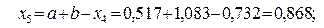
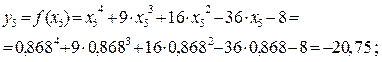
Так как 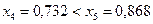 , и
, и 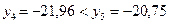 , то правый отрезок
, то правый отрезок 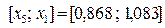 отбрасываем и считаем, что
отбрасываем и считаем, что 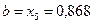 , а
, а 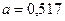 не меняется.
не меняется.
Так как 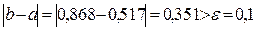 , то нужно выполнить следующее приближение.
, то нужно выполнить следующее приближение.
5) Теперь по правилу «золотого сечения» делим отрезок 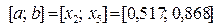 , причем точка
, причем точка 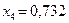 уже находится внутри этого отрезка, а точку
уже находится внутри этого отрезка, а точку 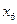 ищем как точку, симметричную точке
ищем как точку, симметричную точке 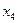 относительно середины отрезка
относительно середины отрезка 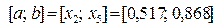 , т.е. по формуле
, т.е. по формуле
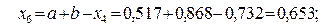
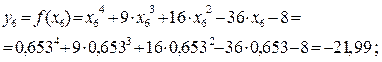
Так как 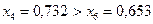 , и
, и 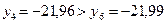 , то правый отрезок
, то правый отрезок 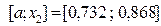 отбрасываем и считаем, что
отбрасываем и считаем, что 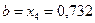 , а
, а 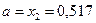 не меняется.
не меняется.
Так как 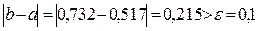 , то нужно выполнить следующее приближение.
, то нужно выполнить следующее приближение.
6) Теперь по правилу «золотого сечения» делим отрезок 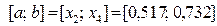 , причем точка
, причем точка 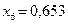 уже находится внутри этого отрезка, а точку
уже находится внутри этого отрезка, а точку 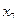 ищем как точку, симметричную точке
ищем как точку, симметричную точке 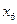 относительно середины отрезка
относительно середины отрезка 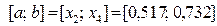 , т.е. по формуле
, т.е. по формуле
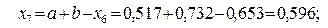
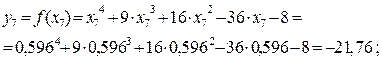
Так как 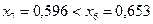 , а
, а 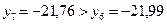 , то левый отрезок
, то левый отрезок 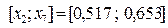 отбрасываем и считаем, что
отбрасываем и считаем, что 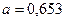 , а
, а 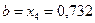 не меняется.
не меняется.
Так как 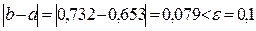 , то процесс последовательных приближений можно считать законченным и середину отрезка
, то процесс последовательных приближений можно считать законченным и середину отрезка 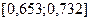 т.е. точку
т.е. точку 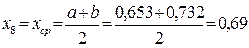 принять за решение.
принять за решение.
Итак, 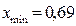 ; число приближений
; число приближений  .
.
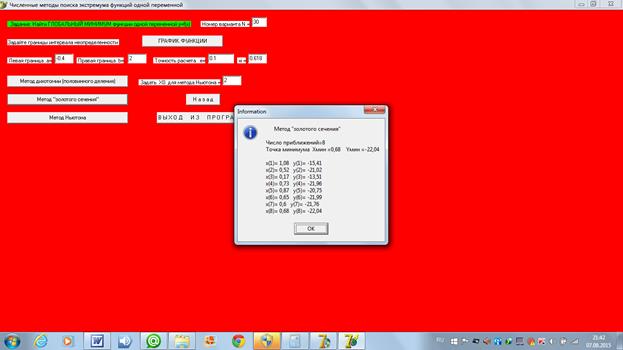
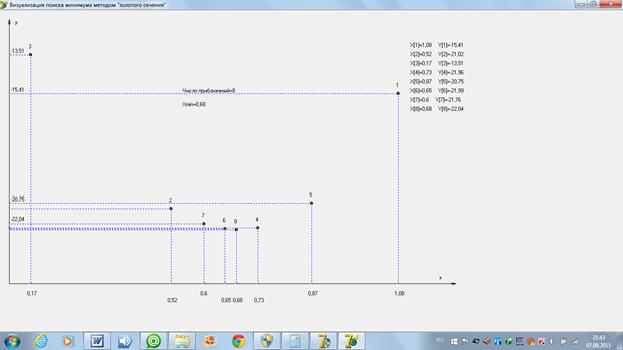
Ниже приведены расчеты нахождения минимума функции методом «золотого сечения», выполненные с помощью компьютерной программы.
 2015-10-22
2015-10-22 1020
1020








