Для метода Ньютона нужно задать начальное приближение 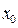 из условия
из условия
 , иначе процесс сходимости не гарантирован.
, иначе процесс сходимости не гарантирован.
Если  , то
, то 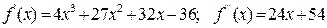 и
и 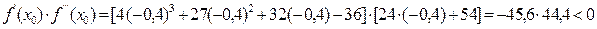 .
.
Если 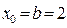 , то
, то 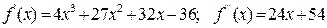 и
и  .
.
Следовательно, в качестве начального приближения следует выбрать точку 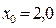 .
.
1) Находим первое приближение по формуле
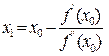

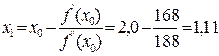
 ;
;
Так как  , то требуется второе приближение.
, то требуется второе приближение.
2) Находим второе приближение по формуле



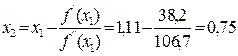

Так как  , то требуется третье приближение.
, то требуется третье приближение.
3) Находим третье приближение по формуле
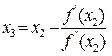



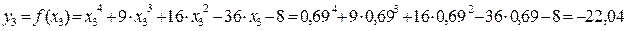
Так как  , то процесс последовательных приближений можно считать законченным и значение
, то процесс последовательных приближений можно считать законченным и значение  принять за точку минимума.
принять за точку минимума.
Итак, 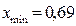 ; число приближений
; число приближений  .
.
Ниже приведены расчеты нахождения минимума функции методом Ньютона, выполненные с помощью компьютерной программы.


Заметим, что в случае выбора за начальное приближение точки  , процесс все же сойдется, но за большее число приближений.
, процесс все же сойдется, но за большее число приближений.


Результаты всех расчетов сведем в таблицу
| № | Название метода поиска | Число приближений | Точка минимума |
| Метод дихотомии | (0,69; -22,04) | ||
| Метод «золотого сечения» | (0,68; -22,04) | ||
| Метод Ньютона | (0,69; -22,04) |
Выводы: При поиске минимума функции  на отрезке
на отрезке
 самым быстрым оказался метод Ньютона (4 приближения).
самым быстрым оказался метод Ньютона (4 приближения).
6 Лабораторная работа №6. Численное решение обыкновенных дифференциальных уравнений методами Эйлера, модифицированного метода Эйлера с пересчетом, Рунге-Кутты.
Задание.
Методами Эйлера, модифицированным методом Эйлера с пересчетом и методом Рунге-Кутты 4-го порядка найти частное решение обыкновенного дифференциального уравнения 1-го порядкавида  , с начальным условием
, с начальным условием  , на интервале
, на интервале 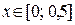 с шагом
с шагом 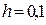 .
.
Решение.
6.1 Найдем сначала точное решение дифференциального уравнения  .
.
Это уравнение сводится к уравнению с разделяющимися переменными с помощью подстановки  . Тогда
. Тогда  и уравнение примет вид
и уравнение примет вид  Разделяя переменные, получим
Разделяя переменные, получим

Частное решение при начальном условии  :
:

Итак, точное решение имеет вид:  .
.
Протабулируем полученное решение на интервале 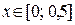 с шагом
с шагом 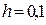 и результаты расчетов сведем в таблицу 6.1
и результаты расчетов сведем в таблицу 6.1

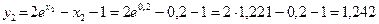

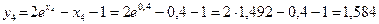

Таблица 6.1 Результаты табулирования функции 
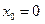 |  |  |  |  |  |
 | 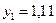 | 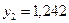 |  | 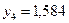 | 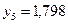 |
6.2 Решение дифференциального уравнения  методом Эйлера.
методом Эйлера.
Итерационная формула метода Эйлера для дифференциального уравнения  имеет вид:
имеет вид:  .
.
У нас  ;
; 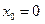 ;
;  ;
; 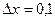 .
.
Результаты расчетов сведены в таблицу 6.2
| Номер точки n |  |  |  |  |
| 0,0 | 1,00 | 0,0+1,00=1,00 |  | |
| 0,1 | 1,10 | 0,1+1,10=1,20 | 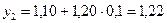 | |
| 0,2 | 1,22 | 0,2+1,22=1,42 |  | |
| 0,3 | 1,36 | 0,3+1,36=1,66 |  | |
| 0,4 | 1,53 | 0,4+1,53=1,93 |  | |
| 0,5 | 1,72 |
6.3 Решение дифференциального уравнения  модифицированным методом Эйлера с пересчетом.
модифицированным методом Эйлера с пересчетом.
Итерационная формула модифицированного метода Эйлера с пересчетом для дифференциального уравнения  имеет вид:
имеет вид:
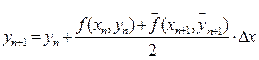 , где
, где 
Результаты расчетов сведены в таблицу 6.3
| № точки n |  |  |  |  |  |
| 0,0 | 1,00 | 0,0+1,00=1,00 |  | 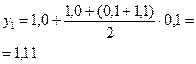 | |
| 0,1 | 1,11 | 0,1+1,11=1,21 |  |  | |
| 0,2 | 1,24 | 0,2+1,24=1,44 |  | 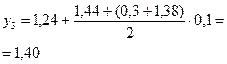 | |
| 0,3 | 1,40 | 0,3+1,40=1,70 |  |  | |
| 0,4 | 1,58 | 0,4+1,58=1,98 |  |  | |
| 0,5 | 1,79 |
6.4 Решение дифференциального уравнения  методом Рунге-Кутты 4-го порядка.
методом Рунге-Кутты 4-го порядка.
Итерационная формула модифицированного метода Эйлера с пересчетом для дифференциального уравнения  имеет вид:
имеет вид:
 где
где
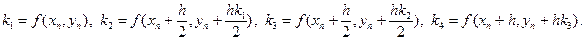
Результаты расчетов сведены в таблицу 6.4
| Номер точки n |  |  |  |  |  |  |  |
| 0,0 | 1,00 | 0+1=1 | 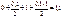 |  | 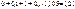 |  | |
| 0,1 | 1,11 | 0,1+1,11=1,21 |  |  | 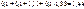 |  | |
| 0,2 | 1,24 | 0,2+1,24=1,44 | 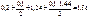 |  | 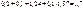 |  | |
| 0,3 | 1,40 | 0,3+1,4=1,7 |  | 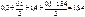 | 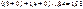 |  | |
| 0,4 | 1,58 | 0,4+1,58=1,98 | 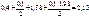 |  |  |  | |
| 0,5 | 1,79 |
 2015-10-22
2015-10-22 3238
3238
