Задание.
С точностью 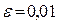 найти все решения системы уравнений
найти все решения системы уравнений 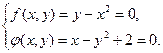 методом Ньютона. Исследовать процесс поиска решения, задаваясь разными значениями нулевого приближения
методом Ньютона. Исследовать процесс поиска решения, задаваясь разными значениями нулевого приближения 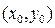 .
.
Решение.
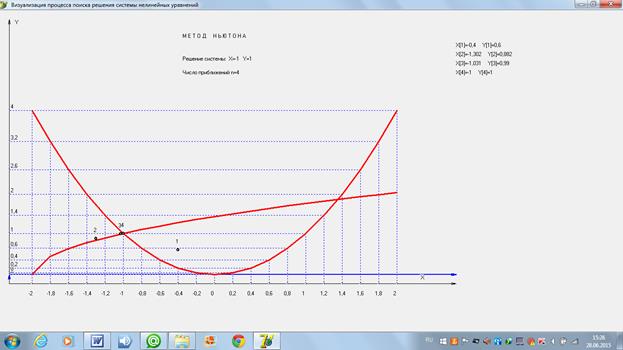
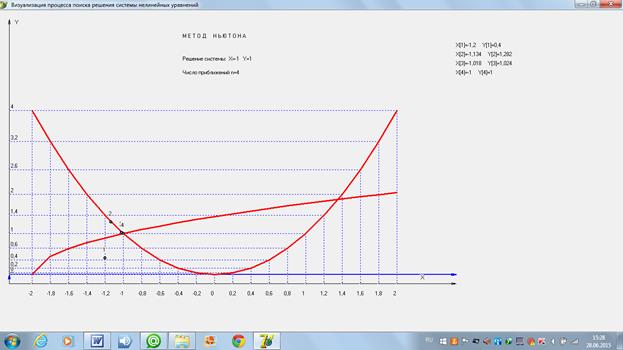
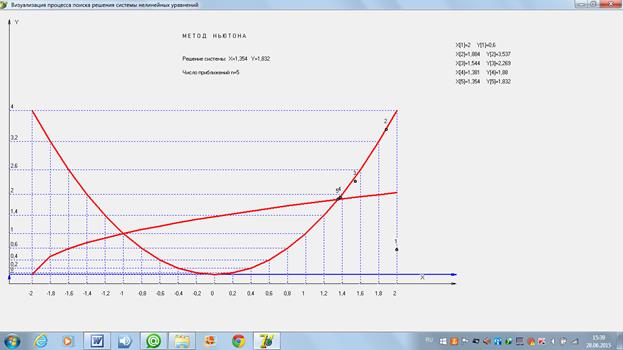
Нарисуем в системе координат XOY графики функций 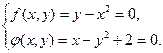
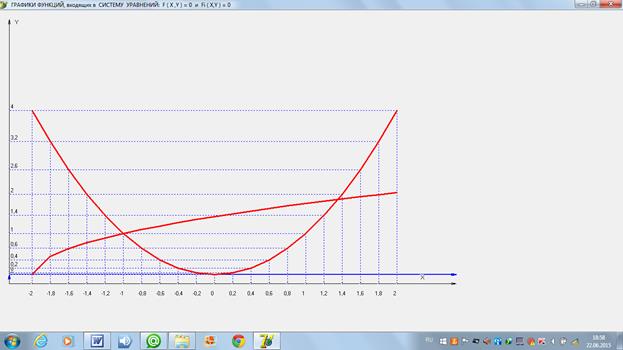
Из графиков функций видно, что система имеет два действительных решения.
4.1 Нахождение первого решения (левой точки, с меньшим значением координаты «x»). Рассмотрим 4 варианта задания нулевого проиближения в каждом из четырех возможных секторов:
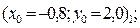
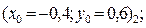
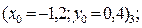
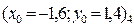
и изобразим картину процесса поиска решения.
1) 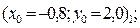
Приведем последовательность расчета первого варианта «вручную».
а) Расчет первого приближения.
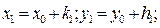
где приращения 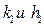 находятся из системы уравнений (5.4)
находятся из системы уравнений (5.4)
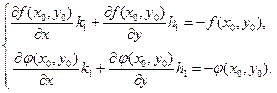
(см. раздел 5.1 теоретической части).
В нашем случае
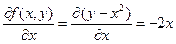 ;
; 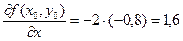 ;
;
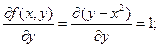
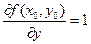 ;
;
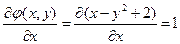 ;
; 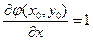 ;
;
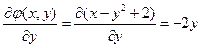 ;
; 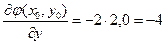 ;
;
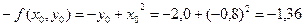 ;
;
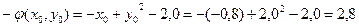 ;
;
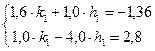
Решим систему линейных уравнений методом Крамера.
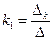 ,
, 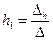 , где
, где
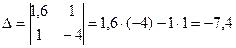 ;
;
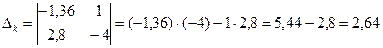 ;
;
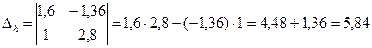 ;
;
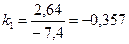 ,
, 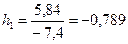 ;
;
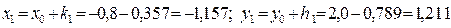 .
.
Так как 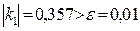 и
и 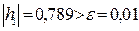 , то точность нахождения решения системы уравнений недостаточна, и необходимо еще одно приближение.
, то точность нахождения решения системы уравнений недостаточна, и необходимо еще одно приближение.
б) Расчет второго приближения.
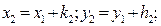
где 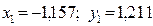 , а приращения
, а приращения 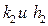 находятся из системы уравнений
находятся из системы уравнений
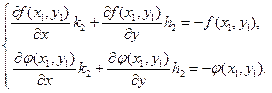
В нашем случае
|
|
|
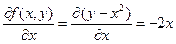 ;
; 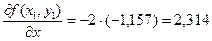 ;
;
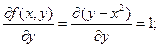
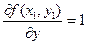 ;
;
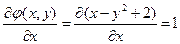 ;
; 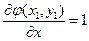 ;
;
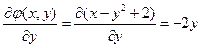 ;
; 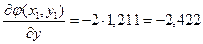 ;
;
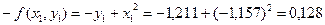 ;
;
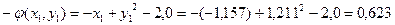 ;
;
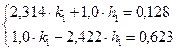
Решим систему линейных уравнений методом Крамера.
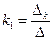 ,
, 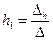 , где
, где
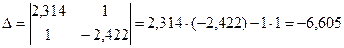 ;
;
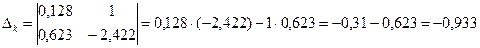 ;
;
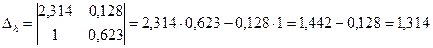 ;
;
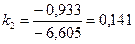 ,
, 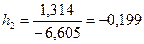 ;
;
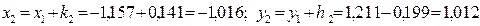 .
.
Так как 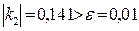 и
и 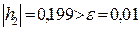 , то точность нахождения решения системы уравнений недостаточна, и необходимо еще одно приближение.
, то точность нахождения решения системы уравнений недостаточна, и необходимо еще одно приближение.
в) Расчет третьего приближения.
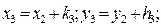
где 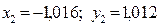 , а приращения
, а приращения 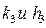 находятся из системы уравнений
находятся из системы уравнений
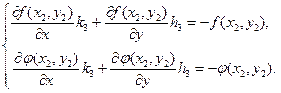
В нашем случае
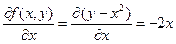 ;
; 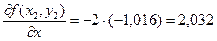 ;
;
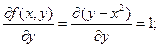
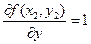 ;
;
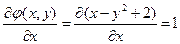 ;
; 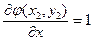 ;
;
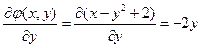 ;
; 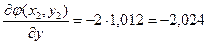 ;
;
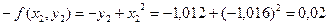 ;
;
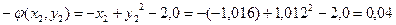 ;
;
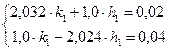
Решим систему линейных уравнений методом Крамера.
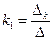 ,
, 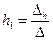 , где
, где
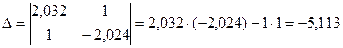 ;
;
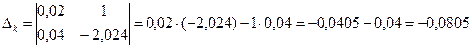 ;
;
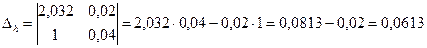 ;
;
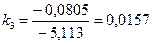 ,
, 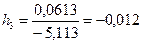 ;
;
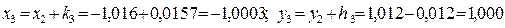 .
.
Так как 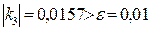 и
и 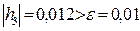 , то точность нахождения решения системы уравнений недостаточна, и формально необходимо сделать еще одно последнее приближение.
, то точность нахождения решения системы уравнений недостаточна, и формально необходимо сделать еще одно последнее приближение.
Итак, решение системы: 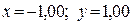 .
.
Ниже приведены расчеты этого и всех других вариантов расчета, выполненные с помощью компьютерной программы.
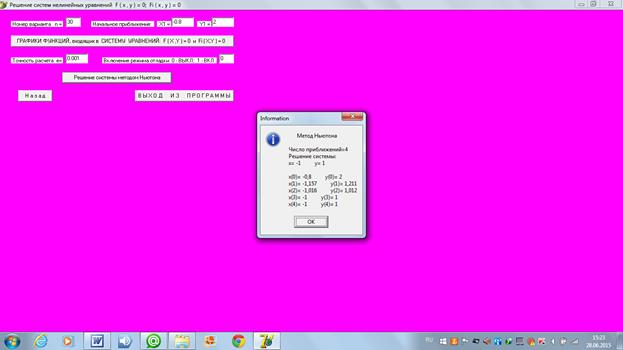
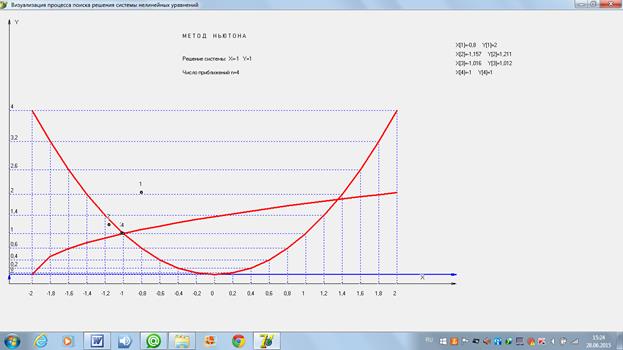
2) 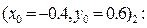
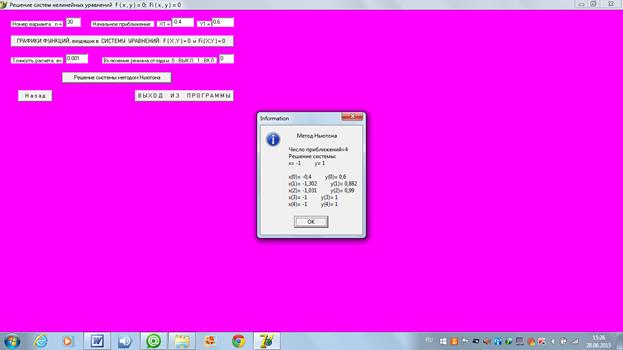
3) 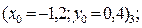
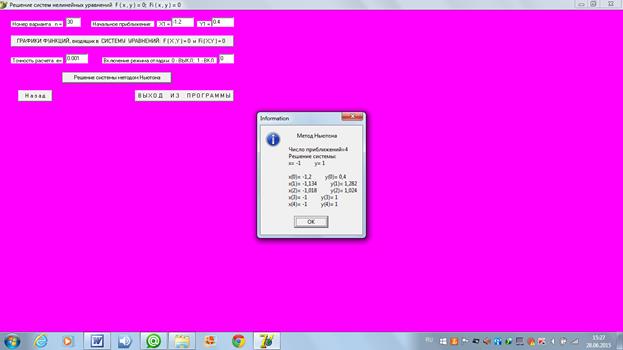
4) 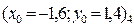 :
:
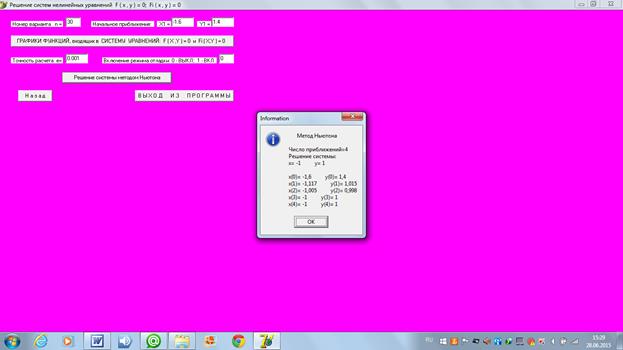
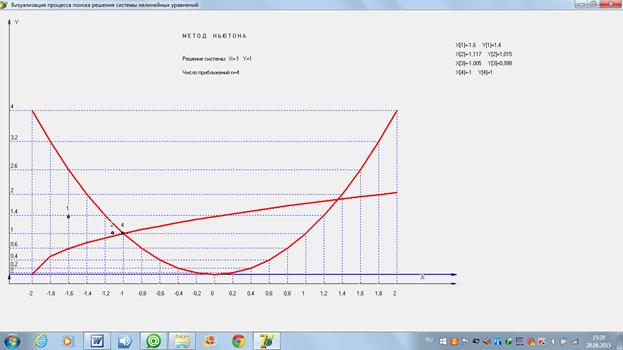
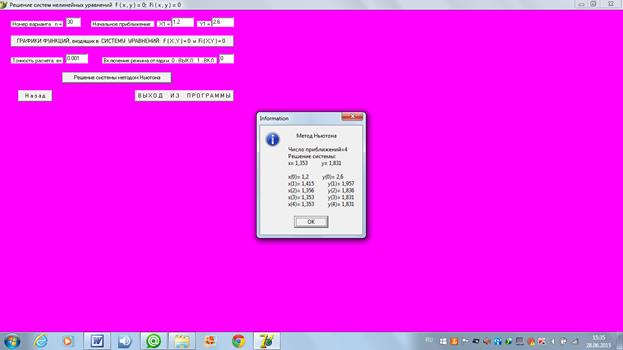
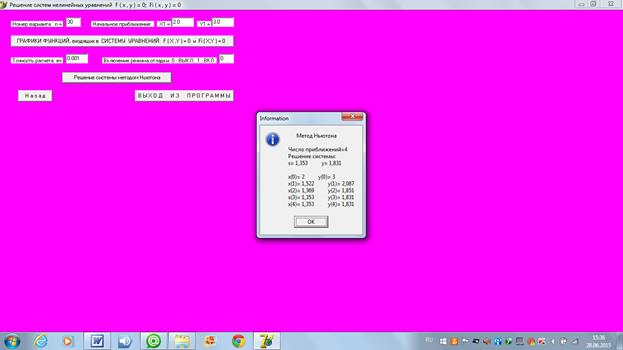
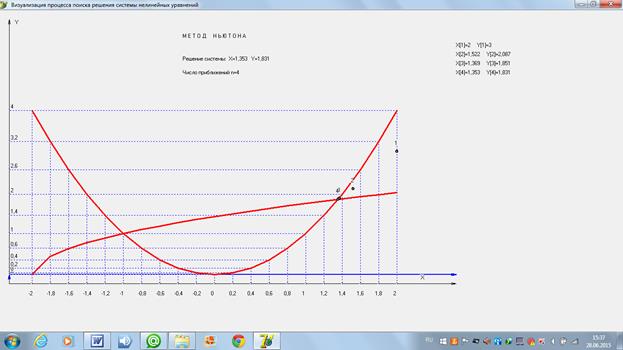
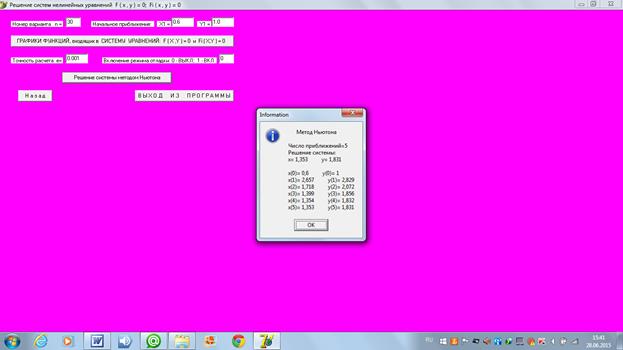
4.2 Нахождение второго решения (правой точки, с большим значением координаты «x»). Рассмотрим 4 варианта задания нулевого проиближения в каждом из четырех возможных секторов:
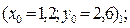
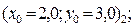
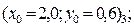
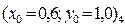
и изобразим картину процесса поиска решения.
1) 
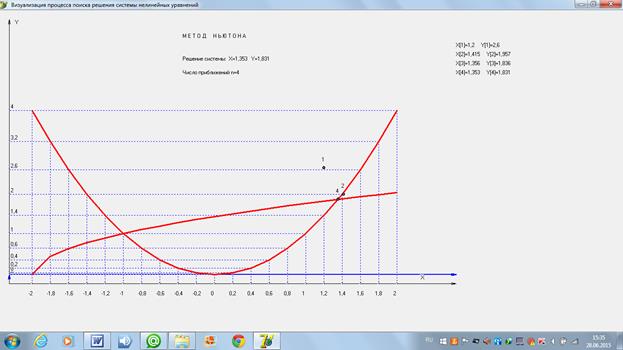
2) 
3) 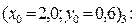
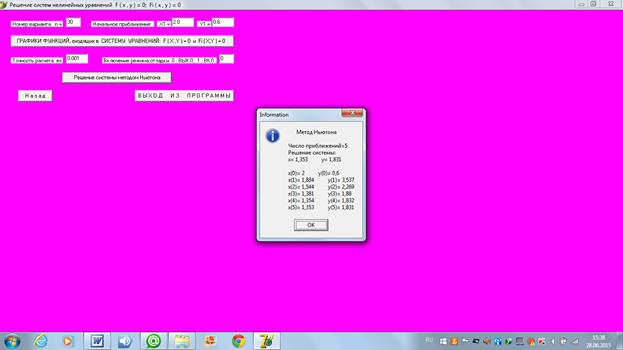
4) 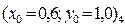 :
:
4.3 Пример задания исходных данных, когда решение методом Ньютона найти не удается. Рассмотрим следующий вариант задания нулевого проиближения:
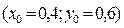
Полученный результат – «Число приближений > 100!!!» говорит о том, что процесс поиска решения расходится.
Выводы: Метод Ньютона быстро приводит к нахождению решения системы уравнений, но он очень чувствителен к заданию нулевого приближения. В случае неудачного задания нулевого приближения процесс поиска может расходиться.
 2015-10-22
2015-10-22 1076
1076
