1) Прежде всего, необходимо проверить условия сходимости метода Ньютона:
а) в интервале поиска корня первая и вторая производные сохраняют знак;
б) нулевое приближение  выбрано из условия
выбрано из условия  .
.
а) Для функции 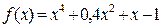 ранее был определен интервал поиска корня
ранее был определен интервал поиска корня 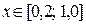 .
.
Первая производная 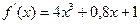 ;
; 
 сохраняет знак, что видно и из графика функции – на выбранном отрезке она монотонно возрастает.
сохраняет знак, что видно и из графика функции – на выбранном отрезке она монотонно возрастает.
Вторая производная  , т.е. кривая вогнута при любых
, т.е. кривая вогнута при любых 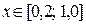 , что так же видно из графика.
, что так же видно из графика.
б) Выберем начальное приближение  и проверим условие
и проверим условие  .
.
При 
 ;
;  ;
; 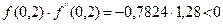 .
.
Точка  не подходит.
не подходит.
При 
 ;
;  ;
;  .
.
Точка  подходит.
подходит.
Итак, за начальное приближение в методе Ньютона следует выбрать точку  .
.
2) Находим значение корня в первом приближении.  . Т.к. длина отрезка
. Т.к. длина отрезка 
 , то точность нахождения корня недостаточна, и потребуется второе приближение.
, то точность нахождения корня недостаточна, и потребуется второе приближение.
3) Находим значение корня во втором приближении.  . Т.к. длина отрезка
. Т.к. длина отрезка 
 , то точность нахождения корня недостаточна, и потребуется третье приближение.
, то точность нахождения корня недостаточна, и потребуется третье приближение.
4) Находим значение корня в третьем приближении.  . Т.к. длина отрезка
. Т.к. длина отрезка 
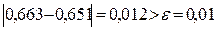 , то точность нахождения корня еще недостаточна, и потребуется четвертое приближение.
, то точность нахождения корня еще недостаточна, и потребуется четвертое приближение.
|
|
|
5) Находим значение корня в четвертом приближении.  . Т.к. длина отрезка
. Т.к. длина отрезка 
 , то с заданной точностью значение
, то с заданной точностью значение 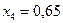 можно принять за решение уравнения.
можно принять за решение уравнения.
6) Решение по компьютерной программе для метода касательных (Ньютона):
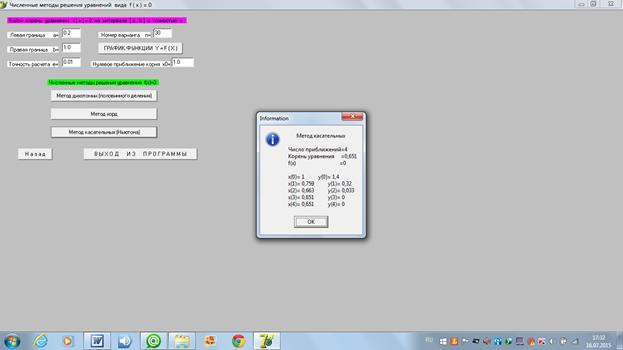

Результаты расчетов заносим в таблицу 3.1:
Таблица 3.1 Нахождение корня уравнения  на отрезке
на отрезке 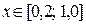
| № | Название метода | Число итераций | Значение корня |
| Дихотомии (половинного деления) | 0,653 | ||
| Хорд | 0,65 | ||
| Касательных (Ньютона) | 0,65 |
Вывод: самым быстрым для данной функции является метод Ньютона.
 2015-10-22
2015-10-22 2349
2349
