Поиск минимума методом дихотомии

1) Первые два приближения возьмем на расстоянии 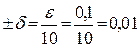от середины выбранного отрезка :

;

.

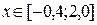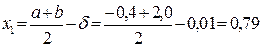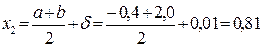Так как 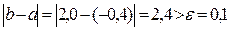, то нужно выполнить следующее приближение.

Значения функции в этих точках

;

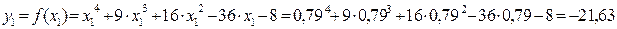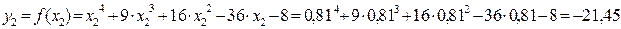
Так как 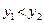, то правый отрезок 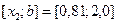отбрасываем, т.е. считаем, что минимум функции находится на отрезке .

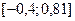Итак, перед второй итерацией считаем, что .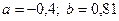

2) Вторые два приближения возьмем на расстоянии 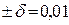от середины отрезка :

;

.

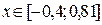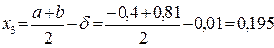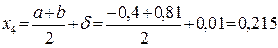Так как 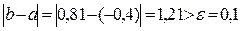, то нужно выполнить следующее приближение.

Значения функции в этих точках

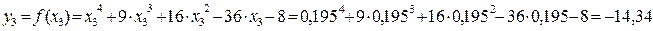
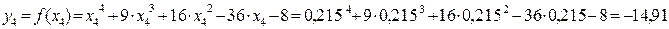Так как 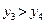, то левый отрезок 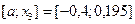отбрасываем, т.е. считаем, что минимум функции находится на отрезке .

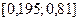Итак, перед третьей итерацией считаем, что .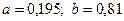

3) Третьи два приближения возьмем на расстоянии 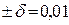от середины отрезка :

;

.

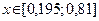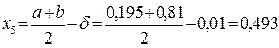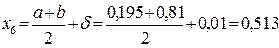Так как 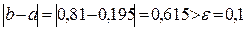, то нужно выполнить следующее приближение.

Значения функции в этих точках

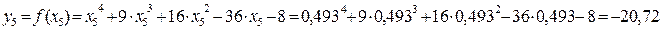
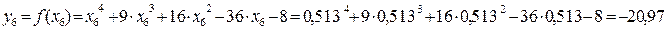Так как 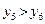, то левый отрезок 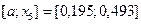отбрасываем, т.е. считаем, что минимум функции находится на отрезке .

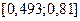Итак, перед четвертой итерацией считаем, что .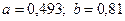

4) Четвертые два приближения возьмем на расстоянии 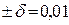от середины отрезка :

;

.

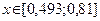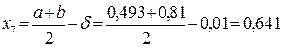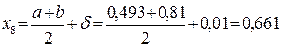Так как 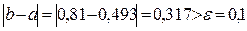, то нужно выполнить следующее приближение.

Значения функции в этих точках

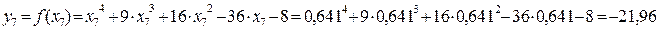
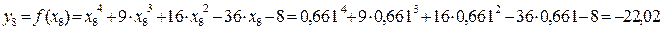Так как 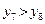, то левый отрезок 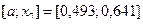отбрасываем, т.е. считаем, что минимум функции находится на отрезке .

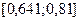Итак, перед пятой итерацией считаем, что .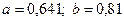

5) Пятые два приближения возьмем на расстоянии 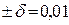от середины отрезка :

;

.

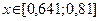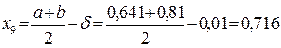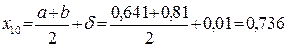Так как 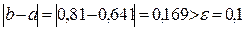, то нужно выполнить следующее приближение.

Значения функции в этих точках

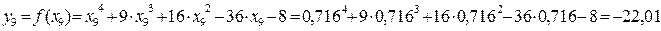
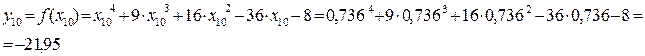Так как 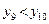, то правый отрезок 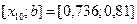отбрасываем, т.е. считаем, что минимум функции находится на отрезке .

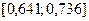Итак, перед шестой итерацией считаем, что .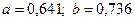

6) Шестые два приближения возьмем на расстоянии 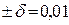от середины отрезка :

;

.

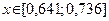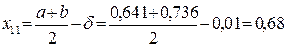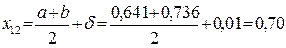Так как 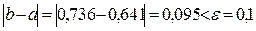, то процесс последовательных приближений можно считать законченным и середину отрезка 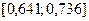т.е. точку 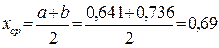принять за решение.

Итак, 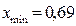; число приближений .

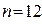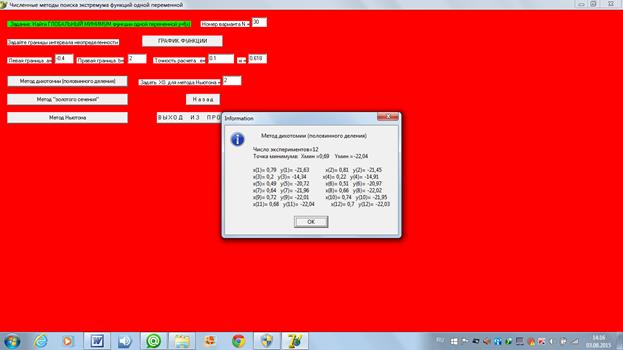
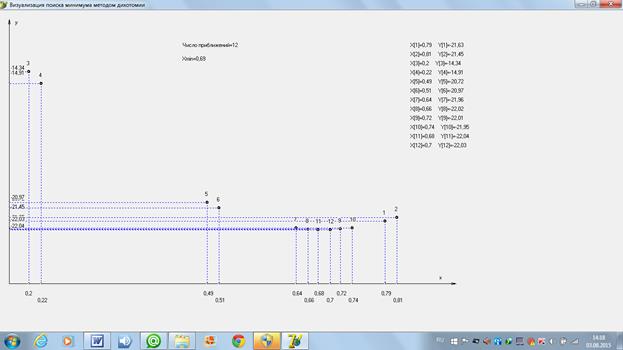
Ниже приведены расчеты нахождения минимума функции методом дихотомии, выполненные с помощью компьютерной программы.