Рассмотрим цилиндр вращающийся вокруг неподвижной оси (Рис. 4.4) под действием постоянной касательной силы 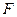 .За время
.За время  точка приложения силы переместится на
точка приложения силы переместится на  и работа этой силы будет
и работа этой силы будет  , которая равна приращению кинетической энергии:
, которая равна приращению кинетической энергии:  , т.к.
, т.к. 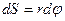 , то
, то
 (4.13)
(4.13)
Величину  , равную произведению проекции силы на плоскость, перпендикулярную оси вращения, на рассотояние до оси вращения (плечо силы
, равную произведению проекции силы на плоскость, перпендикулярную оси вращения, на рассотояние до оси вращения (плечо силы  ), называют моментом силы относительно оси
), называют моментом силы относительно оси  :
:
 , (4.14)
, (4.14)
Тогда вместо (4.13) запишем:
 или
или 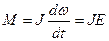 (4.15)
(4.15)
Эта формула выражает основное уравнение динамики вращательного движения: момент силы относительно оси вращения равен произведению момента инерции относительно этой оси на угловое ускорение. Роль силы при вращательном движении играет, момент силы, массы - момент инерции. Момент силы - векторная величина, направленная вдоль оси вращения. Его направление определяется правилом правого винта.
 2015-10-22
2015-10-22 364
364








