Преобразования Лоренца

В С.Т.О. преобразования координат (5.1), описывающие переход от одной И.С.О. к другой, заменяются новыми соотношениями, которые удовлетворяют постоянству скорости света - преоб­разованиями Лоренца. Для частного случая двух систем 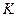и 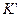, находящихся в относительном движении вдоль оси (Рис. 5.1), они имеют вид:

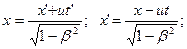
(5.3)

где .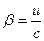

Из этих формул видно, что при малых скоростях для формулы (5.3) переходят в (5.1), следовательно, законы классической физики входят в С.Т.О. как частный случай.

Из преобразований Лоренца вытекают основные следствия.

Замедление времени

В направлении часы, связанные с системой 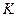, измеряют интервал времени: . При наблюдении в движущейся системе этот интервал становится равным

, (5.4)

Для движущегося наблюдателя время идёт медленнее.

Сокращение длин

Если в системе 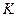находится отрезок , то это же расстояние для движущегося наблюдателя в системе 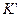окажется равным:

Так как наблюдатель видит в своей системе 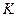оба конца одновременно , то из формул обратного преобразования Лоренца (5.3) получим , откуда следует, что:

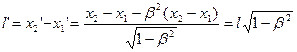, (5.5)

Для движущегося наблюдателя длина отрезка кажется уменьшенной в направлении движения раз, т.е. движущемуся наблюдателю шар кажется сплющенным эллипсоидом.