2015-10-22
315
При вращательном движении точки количественной мерой её движения является момент импульса точки относительно оси, который определяется по формуле:
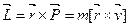, (4.16)
где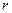 
- радиус окружности, по которой движется точка; 
- её имульс
Момент импульса вращающегося тала равен сумме моментов отдельных его частиц:
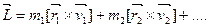
Если ось вращения неподвижна, то момент импульса вращающегося тела можно найти так:
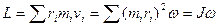, (4.17)
где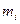 
и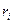 
- масса и радиус вращения 
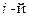точки, 
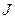- момент
инерции всего тела относительно выбранной оси вращения.
Используя эту формулу, основное уравнение вращательного движения можно записать в виде:
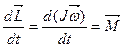, (4.18)
Если на вращающееся тело не действуют внешние силы или их результирующий момент равен нулю, то момент импульса тела относительно оси вращения есть величина постоянная. Из (4.18) пр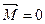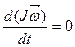и 
:
и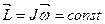 
(4.19)
В изолированной системе полный момент импульса есть величина постоянная. Это есть закон сохранения момента импульса.
| Лекция 7 | Основы релятивистской механики. Постулаты специальной теории относительности. Преобразование Лоренца. |
| Относительность длин и промежутка времени. Преобразование скоростей и ускорений в релятивистской кинематике. Понятие о релятивистской динамике. Закон взаимосвязи массы и энергии. |
