2015-10-22
1025
Если дело вращается вокруг неподвижной оси, то его кинетическая энергия равна:
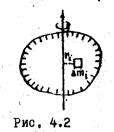
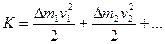(Рис. 4.2.)
Используя формулу (4.4), получим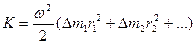 
где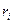 
и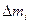 
- расстояние i-частицы тела до оси вращения; 
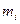- её масса.
Величина, стоящая в скобках, не зависит от скорости движения тела и характеризует инерционные свойства тела во вращательном движении: чем больше эта величина, тем большую энергию надо затратить для достижения данной скорости. Эта величина, характеризующая твердое тело, а также выбранную, ось вращения, называется моментом инерции тала относительно данной оси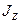 
. Тогда кинетическую энергию можно записать в виде:
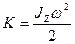(4.9)
Момент инерции тела вычисляют по формуле:
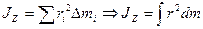(4.10)
Для материальной точки, вращающейся вокруг оси,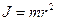 
; для шара, вращающегося вокруг оси, проходящей через его центр, 
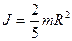.Полная кинетическая энергия катящегося тела вычисляется по формуле:
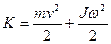(4.11)
Если известен момент инерции относительно оси, проходя через центр инерции тела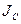 
, можно вычислить момент инерция относительно параллельной оси (теорема Штейнера):
|
|
|
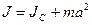, (4.12)
где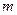 
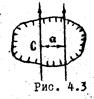
- масса тела,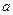 
- расстояние между осями (Рис. 4.3).
