Приклади розв’язання типових задач

Задача 1. Довести, що для будь-якого натурального число ділиться на 7.

Розв’язання.

· Базис індукції. Якщо , то число 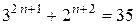ділиться на 7.

· Індукційний крок. Припустимо, що для довільного число ділиться на 7. При 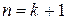маємо

.

Отримане число ділиться на 7, оскільки воно є різницею двох цілих чисел, кожне з яких ділиться на 7 (зменшуване ділиться на 7 за припущенням індукції).

Задача 2. Довести, що для будь-якого натурального має місце тотожність

.

Розв’язання.

· Базис індукції. Якщо , то 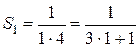, тобто тотожність виконується.

· Індукційний крок. Припустимо, що тотожність вірна для , тобто

.

Доведемо тотожність для .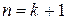

,

що і треба було довести.

Задача 3. Довести, що для будь-якого натурального .

Розв’язання.

· Базис індукції. Якщо , то , тобто твердження вірне.

· Індукційний крок. Нехай при дана нерівність виконується, тобто . Доведемо справедливість нерівності при 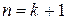. Маємо:

.

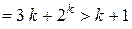Отже, на основі принципу математичної індукції дане твердження доведене для будь-якого натурального .

A1

1. Довести, що ділиться на 6 для будь-якого натурального .

2. Довести, що

для будь-якого натурального .

3. Обчислити суму .

4. Довести, що для довільного натурального виконується нерівність .

5. Нехай 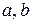та відповідно катети та гіпотенуза прямокутного трикутника. Довести, що для будь-якого натурального .

B1

1. Довести, що для будь-якого натурального число ділиться на 23.

2. Довести, що .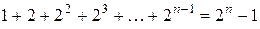

3. Довести, що

.

4. Довести, що сума кубів трьох послідовних натуральних чисел ділиться на 9.

5. Довести, що для будь-якого натурального число ділиться на 6.

6. Довести, що .

C1

1. Довести, що для будь-якого натурального .

2. Довести, що різних прямих, які проходять через одну точку ділять площину на частин.

3. Довести, що для будь-якого натурального

.

4. Довести, що для будь-якого натурального

.

5. Довести, що

.

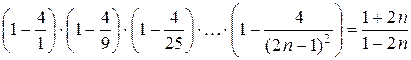Множини