2015-10-22
1885
Нехай задано функцію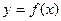 
, яка діє з множини Г в множину 
:
,
a функція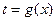 
діє з множини Х в Г:
,
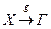то кажуть, що задано складну функцію 
, яка діє з множини Х в множину (або композиція функцій f і g: 
).
Причому функція f – називається зовнішньою, g – внутрішньою функцією.
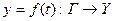
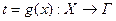
(новий закон)
Наприклад: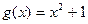 
, 
то 
– складна функція.
Композиція може складатися з більшої кількості функцій.
Функція 
є композицією n функцій, 
– внутрішня функція, 
– проміжні функції, 
– зовнішня функція.
Наприклад: 
– внутрішня, 
– проміжна, 
–
зовнішня.
Озн. Нехай задана функція 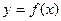, яка діє з області D в область Е 
, якщо кожному елементу у з множини Е за певним законом ставиться у відповідність єдиний елемент х з множини D, то кажуть, що на множині Е задана функція обернена до даної функції .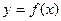
Позн. 
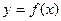– пряма функці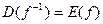я 
– обернена функція 
Але не завжди кожному 
відповідає єдиний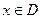 
.
Наприклад: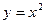 
.
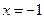
- двозначна функція
Для того, щоб існувало функція 
обернена до функції 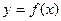(однозначна) необхідно і досить, щоб функція 
мала таку властивість: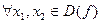 
, тобто різним значенням її аргументу відповідали різні значення функції (одномістна). Прикладом такої функції може бути будь-яка монотонна функція, причому характер монотонності зберігається.
|
|
|
Тому для того, щоб функція мала обернену, необхідно і досить, щоб будь-яка горизонтальна пряма перетинала її графік не більше як в одній точці.
З означення складної й оберненої функції випливають такі рівності
для всіх 
,
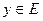для всіх 
.
Зокрема,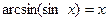 
, якщо 
, 
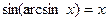, якщо 
,
, якщо 
, 
, 
.
Графік оберненої функції співпадає з графіком прямої функції 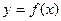. Якщо ж для оберненої функції використати традиційне позначення незалежної і залежної змінних, тобто замінити х на у і у на х, то графіком функції буде множина точок координат площини, яка симетрична до графіка функції 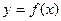відносно прямої y=x (оскільки точки (х;у) і (х;у) координатної площини хОу симетричні відносно прямої y=x).
Якщо графік функції симетричний відносно прямої у=х, то вона обернена сама до себе.
Наприклад: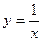 
.
Таким чином, якщо функція 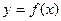і – взаємно обернені і монотонно зростають на області визначення, то точки перетину їх графіків (якщо вони існують) лежать на прямій у=х.
Для знаходження оберненої функції потрібно розв’язати рівняння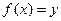 
, подати його розв’язок у вигляді 
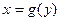і при необхідності перейти до звичайних позначень 
.
Наприклад: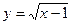 
, 
, 
, 
, 
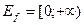
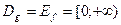– область визначень оберненої функції
– область значень оберненої функції
, 
, – обернена функція,
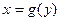– обернена функція в традиційних позначеннях.
Графіки функцій і 
симетричні відносно прямої у=х.
Вправи
1. Які з даних функцій періодичні? Знайти для періодичних функцій найменший додатній період:
|
|
|
1) 
Функція періодична. 
.
2) 
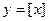
Функція не є періодичною.
2. Дослідити на парність і непарність функції:
1) 
; 
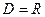Отже, функція непарна.
2) 
; 
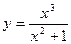
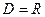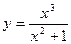. Отже, функція непарна.
3) 
. 
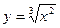
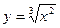. Отже, функція парна.
4) 
. .
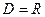. Отже, функція 
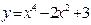парна.
5) 
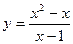
Область визначення має бути симетричною відносно нуля, щоб функція могла бути парною або непарною.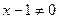 
, 
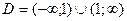, тому D несиметрична відносно осі Оу або точки 0, тому функція не є ні парною, ні непарною.
6) 
. 
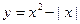
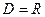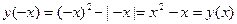. Отже, функція 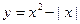парна.
7) 
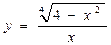
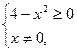
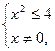
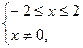
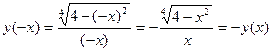. Отже, функція 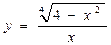непарна.
8) 
. 
.
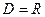Отже, функція непарна.
Функція у=f(х) називається неперервною в точці х0є(а;b), якщо існує границя функції в цій точці, яка дорівнює значенню функції в точці х0.
Отже, функція у=f(х) в точці х0 буде неперервною тоді й тільки тоді, коли виконуються такі умови:
1. функція у=f(х) визначена в точці х0, тобто існує число f(х0);
2. існує границя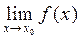 
функції в точці х0;
3. границя функції дорівнює значенню функції в цій точці, тобто
.
Якщо функція у=f(х) є неперервною в кожній точці деякого інтервалу (а;b), то вона називається неперервною в цьому інтервалі.
