Основні означення
Означення. Числовою матрицею розмірності mxn називається прямокутна таблиця із mn чисел, розташованих у m рядках і n стовпцях.
Матрицю позначають так:


A=( ) (i=1…m, j=1…n)
) (i=1…m, j=1…n)
Числа, з яких складена матриця, називаються елементами матриці.
Дві матриці називаються рівними, якщо вони мають однакові розміри й елементи однієї матриці дорівнюють відповідним елементам другої матриці
 , якщо
, якщо 

Матриця, всі елементи якої дорівнюють нулю, називається нульовою, позначається 0.
Матриця, у якої кількість рядків дорівнює кількості стовпців, називається квадратною.
(i=1…m, j=1…m)  .
.
У квадратній матриці елементи  складають головну діагональ, а елементи
складають головну діагональ, а елементи  – допоміжну діагональ.
– допоміжну діагональ.
Квадратна матриця, у якої всі елементи, що розміщені не на головній діагоналі, дорівнюють нулю, називається діагональною.

Діагональна матриця, у якої всі елементи головної діагоналі дорівнюють одиниці, називається одиничною.

Квадратна матриця називається трикутною, якщо всі елементи, розміщені по один бік (або нижче, або вище) від головної діагоналі, дорівнюють нулю.


Квадратна матриця А=  називається симетричною, якщо
називається симетричною, якщо 
 .
.
Приклад симетричної матриці  .
.
Дії над матрицями
Означення. Сумою двох матриць
 і
і 
називається матриця

елементи якої є сумою відповідних елементів матриць A і B, тобто
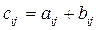
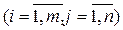 .
.
Сумою трьох і більшої кількості матриць є матриця, яку здобувають послідовним додаванням цих матриць.
Зауваження. Операцію додавання матриць можна виконувати тільки для матриць однакових розмірів.
Приклад
Знайти матрицю C=A+B
 ;
;  ;
;
 .
.
Означення. Добутком матриці A на число  називається матриця B, елементи якої дорівнюють добутку відповідних елементів матриці A на число
називається матриця B, елементи якої дорівнюють добутку відповідних елементів матриці A на число  , тобто
, тобто

 .
.
Приклад. 

Знайти B=3A
B=3A =3  =
=  .
.
Означення. Різницею матриць A–B є матриця, яку знаходять таким чином:
A–B=A+(–B)
Властивості лінійних операцій над матрицями:
1. A+B=B+A
2. (A+B) +C=A+ (B+C)
3. A +0=0+ А=A
4. A +(–A) = 0
5. 1∙ A=A
6. 
7. ∙(A+B)=∙A+∙B
8. 
 .
.
Означення. Матриця A називається узгодженою з матрицею B, якщо кількість стовпців матриці A дорівнює кількості рядків матриці B, тобто
 а
а  .
.
Множити матрицю A на матрицю B можна тільки в тому разі, коли матриця A є узгодженою з матрицею B.
Означення. Добутком матриці  на матрицю
на матрицю  називається матриця
називається матриця  така, що
така, що
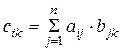
 .
.
Із означення випливає, що елемент матриці C, який стоїть на перетині i -го рядка та k -го стовпця, дорівнює сумі добутків елементів i -го рядка матриці A на відповідні елементи k -го стовпця матриці B.
Приклад.
Знайти C=A∙B, якщо


Матриці A і B узгоджені, так як  , а
, а  . У результаті отримаємо
. У результаті отримаємо 


Таким чином,  .
.
Властивості добутку матриць:
1. A∙E=E∙A=A, Е – одинична матриця.
2. A∙0=0∙A=0, 0 – нульова матриця.
3. (A∙B)∙C=A∙(B∙C)
4. (A∙B)=(∙A)∙B=A(∙B)
5. (A+B)∙C=A∙C+B∙C
6. C∙(A+B)=C∙A+C∙B.
=const.
Означення. Матриця, яку дістають із даної, замінюючи кожний її рядок стовпцем із тим самим номером, називається матрицею, транспонованою до даної і
позначається  , тобто
, тобто



Операція знаходження матриці, транспонованої до даної, називається транспонуванням матриці.
Приклад.
Знайти 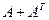 , якщо
, якщо  ,
,  .
.
 .
.
Властивості транспонування матриць:
1. 
2.  =const
=const
3. 
4. 
 2015-10-22
2015-10-22 1100
1100








