Періодичність функції

Озн. Функцію 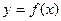називають періодичною на деякій множині , якщо існує таке число Т, що виконуються умови:

. (необхідна) ,

. (достатня) .

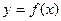Т.1.1. якщо число є періодом функції в області 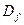, то періодом цієї функції буде і число ,

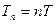Таким чином, якщо функція 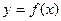має період T, то вона має нескінченне число періодів . Найбільшого періоду немає.

Загалом періодом функції прийнято називати найменший (головний, основний) з періодів.

Період функцій , ,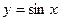

, , ,

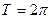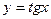– дробова частина .

Проте не завжди періодична функція має найменший період. Так, функція , де с – константа, задовольняє всім умовам визначення

періодичної функції, але не має найменшого періоду.

При дослідженні функцій на періодичність зручно починати його з перевірки виконання необхідних умов, а при їх виконанні – достатні умови розглядають, як рівняння для визначення періоду функції. Важливо врахувати, що період функції стале число, а, отже, не повинно залежати від значень незалежної змінної.