Парні і непарні функції

Озн. Функція 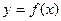називається парною (непарною), якщо для довільного значення виконуються умови:

1. (необх): , тобто область визначення симетрична відносно початку координат;

2. (достатня): – для парної;

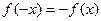– для непарної.

Наприклад: 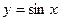, , 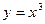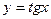–непарні;

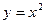, – парні.

Озн. Функції, які не є парними або непарними називаються функціями загального вигляду.

Наприклад: 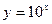, , 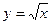ні парні, ні непарні, тобто функції загального вигляду.

Властивості:

1. Графік парної функції симетричний відносно осі Оу

2. Графік непарної функції симетричний відносно початку координат

3. Сума скінченої кількості парних (непарних) функцій, визначених на симетричній множині, є функція парна (непарна) на цій множині.

4. Добуток скінченої кількості парних функцій, визначених на симетричній множині, є функція парна на цій множині.

5. Добуток парної (непарної) кількості непарних функцій, визначених на симетричній множині, є парна (непарна) функція на цій множині.

6. Частка двох парних або непарних функцій f і g, визначених на симетричній множині, є парна функція на цій множині.