1.Визначник матриці, отриманої з даної транспонуванням, дорівнює визначнику цієї матриці.
Доведемо властивості для визначників другого порядку.
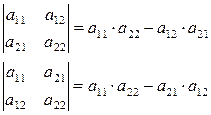
Бачимо, що 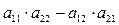 =
= 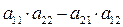 .
.
Приклад.
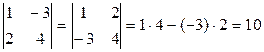 .
.
2.Якщо всі елементи деякого рядка(стовпця) дорівнюють нулю, то сам визначник дорівнює нулю.
Доведення: 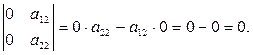
3. Якщо всі елементи деякого рядка(стовпця) визначника мають спільний множник, то його можна винести за знак визначника.
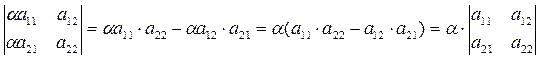 .
.
Приклад.
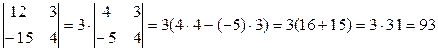
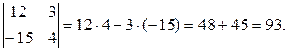
4. Величина визначника не змінюється, якщо до елементів одного рядка (стовпця) додати відповідні елементи другого рядка (стовпця), помножені на одне й те саме число.
Доведення:
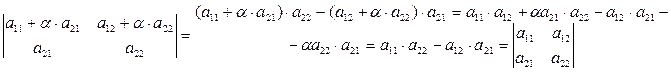 Приклад.
Приклад.
Обчислимо 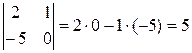
Обчислимо 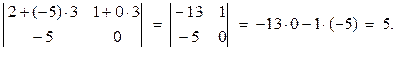
5. Якщо поміняти місцями два рядки (стовпці) визначника, то знак визначника зміниться на протилежний.
Приклад.
Обчислимо 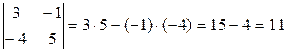 .
.
Тепер обчислимо 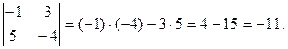
6. Якщо визначник має два пропорційних рядка (стовпця), то визначник дорівнює нулю.
Доведення.
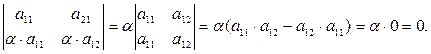
Означення. Якщо у визначнику n-го порядку викреслити один рядок і один стовпчик, на перетині яких стоїть деякий елемент 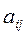 , то одержимо визначник
, то одержимо визначник 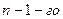 порядку, який називається мінором визначника, відповідного елемента
порядку, який називається мінором визначника, відповідного елемента 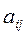 . Позначається
. Позначається 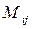 .
.
Означення. Алгебраїчним доповненням елемента 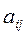 є число
є число 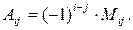
Приклад.
Нехай дано визначник третього порядку. Знайти 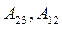 .
.
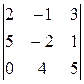
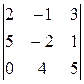
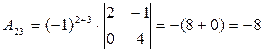
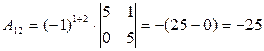 .
.
7. Визначник матриці дорівнює сумі добутків елементів деякого рядка (стовпця) на алгебраїчні доповнення цих елементів.
Доведення(для визначника 3-го порядку)
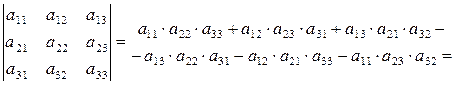
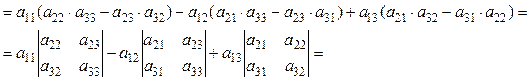
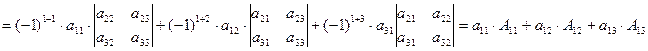 Приклад.
Приклад.
Обчислити 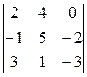 .
.
Розв’язання:
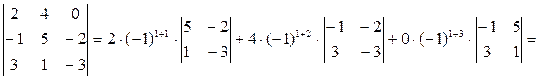
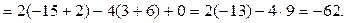
8. Визначник, у якого кожний елемент деякого рядка (стовпця) є сумою двох доданків, дорівнює сумі визначників, у першому з яких у вказаному рядку (стовпці) стоять перші доданки, а у другому – другі доданки; всі інші рядки(стовпці) у обох визначників однакові.
Доведення:
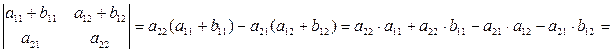
= 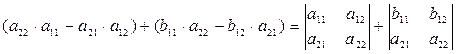 .
.
Зауваження.
Всі властивості визначників другого і третього порядку справедливі і для визначників n-го порядку.
Приклад.
Обчислити визначник четвертого порядку.
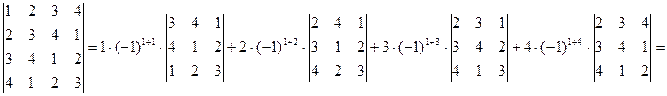 =(9+8+8-1-12-48)-2(6+6+32-4-8-36)+3(24+24+3-16-4-27)-4(16+12+12-6-2-54)=160.
=(9+8+8-1-12-48)-2(6+6+32-4-8-36)+3(24+24+3-16-4-27)-4(16+12+12-6-2-54)=160.
Обернена матриця.
Означення. Квадратна матриця називається невиродженою, якщо її визначник відмінний від нуля.
Означення. Матриця 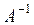 називається оберненою до матриці
називається оберненою до матриці 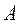 , якщо справджується рівність:
, якщо справджується рівність:
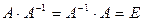 , де
, де 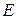 – одинична матриця.
– одинична матриця.
Обернена матриця існує тільки для невиродженої квадратної матриці.
Означення. Союзною до матриці А називається матриця С вигляду:
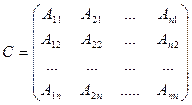 ,
,
де 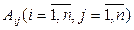 –алгебраїчні доповнення елементів
–алгебраїчні доповнення елементів 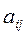 матриці А.
матриці А.
План отримання оберненої матриці:
а) знаходимо визначник матриці А;
б) якщо detA≠0, то знаходимо алгебраїчні доповнення для елементів матриці А;
в) записуємо союзну матрицю С;
г) знаходимо обернену матрицю 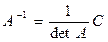 ;
;
д) робимо перевірку, тобто 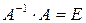 .
.
Приклад. Знайти матрицю, обернену до матриці А.
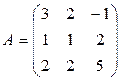
Розв’язання.
а) знаходимо визначник матриці А:
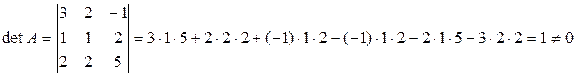
Визначник відмінний від нуля, таким чином матриця А є невиродженою, тому існує обернена матриця.
б) знаходимо союзну матрицю, для цього шукаємо алгебраїчні доповнення елементів 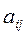 матриці А.
матриці А.
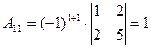
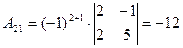
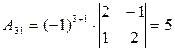
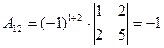
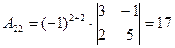
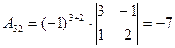
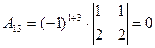
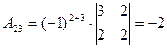
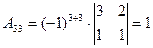 .
.
Маємо:
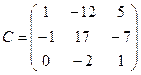 .
.
в) знаходимо обернену матрицю 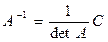
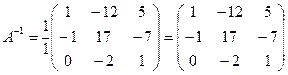 .
.
г) зробимо перевірку, тобто 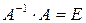 :
:
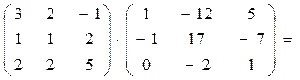
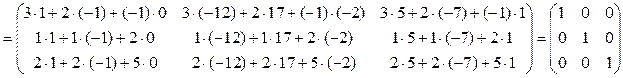
 2015-10-22
2015-10-22 872
872








