Розглянемо довільну систему m лінійних рівнянь з n невідомими (1). Виберемо ведуче рівняння системи. Нехай це буде перше рівняння. Виберемо ведучий елемент  .
.
Розділимо кожний член ведучого рівняння на 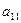 . Тоді система матиме вигляд:
. Тоді система матиме вигляд:
 (2),
(2),
де 
 .
.
Виключимо із 2, 3,, m рівнянь системи (2)  . Для цього перше рівняння помножимо на
. Для цього перше рівняння помножимо на  і додамо до другого рівняння, потім перше рівняння системи помножимо на
і додамо до другого рівняння, потім перше рівняння системи помножимо на  і додамо до третього рівняння. І так далі.
і додамо до третього рівняння. І так далі.
Після цього система набирає вигляду:
 (3),
(3),
де 
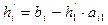
 .
.
Це перший крок.
Запишемо без змін перше рівняння системи (3) і виберемо друге рівняння за основне, а твірним елементом нехай буде  .
.
Розділимо кожний член основного рівняння на 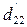 .
.
Тоді система (3) матиме вигляд:
 (4),
(4),
де 
 ,
, 
 .
.
Виключимо з 3, 4,…, m рівнянь системи (4) змінну 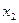 аналогічно першому кроку.
аналогічно першому кроку.
 (5),
(5),
де 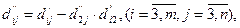
 .
.
Аналогічно попередньому з рівнянь послідовно виключаються змінні  .
.
Виконана операція називається прямим ходом методу Гаусса.
Після цього використовується зворотній хід.
Із останнього рівняння визначається 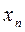 .
.
Після підстановки 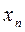 у m-1 рівняння системи визначимо
у m-1 рівняння системи визначимо  .
.
Виконуючи аналогічні операції, знайдемо розв’язок системи.
Приклад.Розв’язати систему рівнянь методом Гаусса.

Розв’язання:

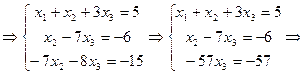
 .
.
 2015-10-22
2015-10-22 457
457








