2015-10-22
430
Вариант №1
- Даны матрицы А и В:
. Найти: 
.
2. Решить СЛУ методом Крамера и методом Гаусса: 
3. Дан треугольник АВС: А (-1; 3), В (4; 2), С (2; -6). Требуется составить уравнение высоты проведенных из вершины А и вычислить ее длину.
4. Найти собственные значения и собственные векторы матрицы 
5. Для числа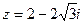 
найти тригонометрическую форму.
6. Исследовать на знакоопределенность квадратичную форму: 
.
7. Даны четыре вектора 
и 
в некотором базисе. Показать, что векторы 
образуют базис, и найти координаты вектора 
в новом базисе.
Вариант №2
1. Даны матрицы А и В: 
. Найти: 
.
2. Решить СЛУ методом Крамера и методом Гаусса: 
3. Дан треугольник АВС: А (1; -1), В (4; 3), С (-2; 5). Требуется составить уравнение медианы АМ, вычислить ее длину.
4. Найти собственные значения и собственные векторы матрицы 
5. Найти сумму и произведение комплексных чисел z 1= 2 – i и z 2 = – 4 + 3 i.
6. Исследовать на знакоопределенность квадратичную форму: 
.
7. Даны четыре вектора 
и 
в некотором базисе. Показать, что векторы образуют базис, и найти координаты вектора в новом базисе.
Вариант №3
1. Даны матрицы А и В: 
. Найти .
2. Решить СЛУ методом Крамера и методом Гаусса: 
3. Дан треугольник АВС: А (-4; -2), В (4; -4), С (2; 5). Требуется составить уравнение высоты проведенных из вершины С и вычислить ее длину.
4. Найти собственные значения и собственные векторы матрицы
5. Выполнить умножение: 
6. Исследовать на знакоопределенность квадратичную форму: 
.
7. Даны четыре вектора 
и 
в некотором базисе. Показать, что векторы образуют базис, и найти координаты вектора в новом базисе.
Вариант №4
1. Даны матрицы А и В: 
. Найти .
2. Решить СЛУ методом Крамера и методом Гаусса: 
3. Дан треугольник АВС: А (2; 8), В (-4; 4), С (-2; -3). Требуется составить уравнение медианы СМ, вычислить ее длину.
4. Найти собственные значения и собственные векторы матрицы 
5. Найти z1z2 и 
, результат написать в алгебраической форме, если 
.
6. Исследовать на знакоопределенность квадратичную форму: 
.
7. Даны четыре вектора 
и 
в некотором базисе. Показать, что векторы образуют базис, и найти координаты вектора в новом базисе.
Критерии выставления баллов за контрольную работу в соответствии с балльно-рейтинговой системой приведены в следующей таблице. Полнота и правильность решений оценивается с точки зрения применения полученных знаний и математических методов к решениям конкретных задач, на основе знаний, умений и навыков, полученных на лекционных, практических занятиях и при выполнении самостоятельной работы по данному модулю.
| Кол-во баллов | Критерии оценки контрольных работ №1-2 | Формируемые компетенции |
| 15-13 баллов | Даны полные и правильные решения на 85-100% задач контрольной работы. Студент показывает умение правильно применять математический аппарат и знания к конкретным ключевым задачам, демонстрирует сформированность всех компетенций. | ПК-4 |
| 13-9 баллов | Даны правильные решения на 70-84% задач контрольной работы. В остальных задачах есть недочеты или несущественные ошибки. Студент показывает умение применять математический аппарат к конкретным ключевым задачам, демонстрирует наличие основных компетенций. | ПК-4 |
| 9-5 баллов | Даны правильные решения на 50-69% задач контрольной работы. В остальных задачах есть недочеты или существенные ошибки. Студент показывает недостаточные умения применять математический аппарат к конкретным ключевым задачам, демонстрирует некоторое наличие компетенции ПК-4 | ПК-4 |
| 5-3 баллов | Правильно выполнены только 30-49% задач контрольной работы. Студент допускает грубые, существенные ошибки при решениях задач. | ПК-4 |
| 2-0 баллов | Решены правильно менее 30% задач контрольной работы. Либо студент присутствовал на контрольной работе, но не сдал ее преподавателю. | __ |
| Кол-во баллов | Критерии оценки контрольной работы №3 | Формируемые компетенции |
| 10-9 баллов | Даны полные и правильные решения на 85-100% задач контрольной работы. Студент показывает умение правильно применять математический аппарат и знания к конкретным ключевым задачам, демонстрирует сформированность всех компетенций. | ПК-4 |
| 9-7 баллов | Даны правильные решения на 70-84% задач контрольной работы. В остальных задачах есть недочеты или несущественные ошибки. Студент показывает умение применять математический аппарат к конкретным ключевым задачам, демонстрирует наличие основных компетенций. | ПК-4 |
| 7-5 баллов | Даны правильные решения на 50-69% задач контрольной работы. В остальных задачах есть недочеты или существенные ошибки. Студент показывает недостаточные умения применять математический аппарат к конкретным ключевым задачам, демонстрирует некоторое наличие компетенции ПК-4 | ПК-4 |
| 5-3 баллов | Правильно выполнены только 30-49% задач контрольной работы. Студент допускает грубые, существенные ошибки при решениях задач. | ПК-4 |
| 2-0 баллов | Решены правильно менее 30% задач контрольной работы. Либо студент присутствовал на контрольной работе, но не сдал ее преподавателю. | __ |
