В большом ряде моделей процессов и в задачах анализа требуются как оценка имеющегося объекта, так и сравнение между собой различных моделей. Так как матрицы - один из наиболее распространенных способов описания экономических процессов и объектов, то использование их универсальных характеристик удобно для задач эталонного сравнения. Собственные значения и векторы и представляют собой такие характеристики.
Собственным векторомквадратной матрицы А называется вектор 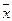
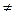 0, удовлетворяющий матричному уравнению А
0, удовлетворяющий матричному уравнению А 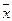 =
= 
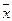 , где
, где  - собственное значение матрицы, соответствующее вектору
- собственное значение матрицы, соответствующее вектору 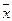 .
.
Представим это равенство в виде
(А-  Е)
Е) 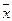 =0.
=0.
Чтобы это однородное матричное уравнение имело ненулевые решения 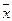 , необходимо и достаточно равенство нулю определителя
, необходимо и достаточно равенство нулю определителя
D(А-  Е)=0.
Е)=0.
Это - характеристическое уравнение (степени n)для матрицы А.
Отсюда получаем сначала собственные значения  , а затем собственные векторы
, а затем собственные векторы 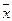 . Общее число этих характеристик равно порядку n матрицы А.
. Общее число этих характеристик равно порядку n матрицы А.
Рассмотрим пример: определить собственные значения матрицы А = 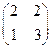 .
.
Составим: А-  Е=
Е= 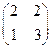 -
-  =
= 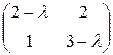 ; D(А-
; D(А-  Е) =
Е) = 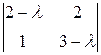 = 0 или
= 0 или
(2-  )(3-
)(3-  )-2=0, откуда получим два собственных значения:
)-2=0, откуда получим два собственных значения: 
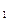 =1;
=1; 
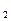 =4.
=4.
Определим собственные векторы для каждого 
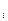 :
:
1.  =1
=1 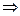
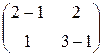
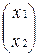 =0, т.е.
=0, т.е. 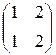
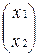 =0 или х
=0 или х 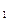 +2 х
+2 х 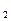 = 0.
= 0.
Собственный вектор определится с точностью до постоянного множителя с. Положим х 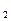 =1, тогда х
=1, тогда х 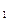 = -2 и
= -2 и 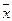
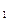 = с
= с 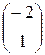 .
.
2.  =4
=4 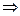
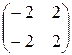
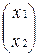 =0 и х
=0 и х 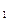 +2 х
+2 х 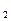 = 0. Полагая х
= 0. Полагая х 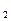 = 1, получим х
= 1, получим х 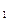 = 1 и вектор
= 1 и вектор 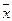
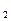 = с
= с 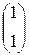 .
.
Вычисленные собственные значения обычно проверяются по их свойствам:
1. Сумма собственных значений равна сумме диагональных элементов матрицы А (следу матрицы А): 
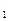 +
+ 
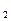 +...
+... 
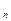 = а
= а 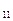 +а
+а 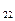 +...+а
+...+а 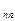 .
.
2. Произведение собственных значений связано с определителем D(A) матрицы А формулой: 
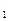


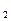 ...
... 

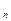 =(-1)
=(-1) 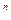 D(A).
D(A).
3. Если матрица А симметрична, то ее собственные значения всегда действительны, т.е. 
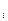
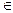 R.
R.
Описанное выше, в целом, представляет собой полную проблему собственных значений - определяются все 
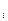 и
и 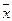
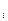 для матрицы А. В большинстве же практических задач это не нужно - итоговое заключение делается по минимальному (или максимальному) собственному значению и соответствующему ему вектору. При этом нет необходимости решать сложное характеристическое уравнение полностью - надо найти только один нужный корень. Такая задача называется частичной проблемой собственных значений. Для ее решения имеются достаточно простые и быстрые методы.
для матрицы А. В большинстве же практических задач это не нужно - итоговое заключение делается по минимальному (или максимальному) собственному значению и соответствующему ему вектору. При этом нет необходимости решать сложное характеристическое уравнение полностью - надо найти только один нужный корень. Такая задача называется частичной проблемой собственных значений. Для ее решения имеются достаточно простые и быстрые методы.
Норма матрицы
Проблема собственных значений определена только для квадратных матриц. В экономической практике часто необходимо оценивать не только квадратные матрицы. Для такой оценки можно использовать универсальное понятие нормы, справедливое для матриц любой размерности.
Нормой произвольной матрицы А называется действительное число 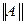 , удовлетворяющее целому ряду условий, наиболее важными из которых являются:
, удовлетворяющее целому ряду условий, наиболее важными из которых являются:
1. 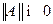 , причем
, причем 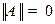 только в случае полностью нулевой матрицы А.
только в случае полностью нулевой матрицы А.
2. 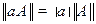 , где
, где 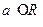 .
.
В какой–то степени норму 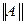 можно образно представлять как показатель “толщины” или “мощности” матрицы А.
можно образно представлять как показатель “толщины” или “мощности” матрицы А.
Норма называется канонической, если 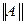
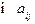 , т.е. она не меньше, по модулю, любого элемента матрицы А. При выборе нормы возможно использовать самые разнообразные соображения, не противоречащие определению. Однако на практике обычно достаточно следующих канонических норм:
, т.е. она не меньше, по модулю, любого элемента матрицы А. При выборе нормы возможно использовать самые разнообразные соображения, не противоречащие определению. Однако на практике обычно достаточно следующих канонических норм:
1. m–норма 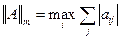 – суммируются, по модулю, все строки матрицы А и максимальная из полученных сумм объявляется нормой.
– суммируются, по модулю, все строки матрицы А и максимальная из полученных сумм объявляется нормой.
2. l–норма 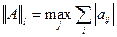 – суммируются, по модулю, все столбцы матрицы А и максимальная из полученных сумм объявляется нормой.
– суммируются, по модулю, все столбцы матрицы А и максимальная из полученных сумм объявляется нормой.
3. k–норма 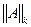 =
= 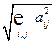 – суммируются квадраты всех элементов матрицы А и корень из этой суммы объявляется нормой.
– суммируются квадраты всех элементов матрицы А и корень из этой суммы объявляется нормой.
Векторы
 2015-10-22
2015-10-22 1854
1854
