Бесконечно малые (б.м.) и бесконечно большие (б.б.) величины

Так как б.м. и б.б. часто встречаются в анализе, то сформулируем их свойства. Для удобства положим a(х) - б.м., b(х) - б.б. величины при х а (или х ).

1. Если функция у=f(х) может быть представлена суммой постоянного числа А и б.м. величины a(х), т.е. у= А +a, то lim y = A и обратно, если lim y = A, то у =А+a.

2. Сумма нескольких б.м. величин тоже является б.м. величиной.

3. Произведение б.м. величины на ограниченную функцию (или число) также является б.м. величиной.

4. Частное от деления б.м. величины на ненулевую ограниченную функцию (или число) является б.м. величиной.

5. Произведение б.б. величины на ограниченную функцию (или число) также является б.б. величиной.

6. Сумма б.б. величины и ограниченной функции (или числа) является б.б. величиной.

7. Частное от деления б.б. величины на ненулевую ограниченную функцию (или число) является б.б. величиной.

8. Величина, обратная б.м. величине, является б.б. величиной: b(х)= 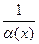; Величина, обратная б.б. величине, является б.м. величиной: a(х)= .

Теоремы о пределах

Для того, чтобы вычислять пределы, разработан ряд удобных теорем, которые приведем без доказательств:

1. Пределпостоянной величины (числа) равен этой постоянной: lim C=C.

2. Пределсуммы равен сумме пределов: lim(u+v-w)=lim u + lim v - lim w.

3. Пределпроизведения равен произведению пределов:

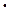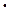lim(u v w)=lim u 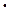lim v lim w.

4. Предел дроби равен частному пределов числителя и знаменателя при условии, что знаменатель - не б.м. величина: lim .

5. В неравенствах можно переходить к пределу, т.е., если u<v (или другой знак неравенства), то lim u <lim v.