Рассмотрим некоторую последовательность, зависящую от натурального аргумента xn=f(n) (n  N), например: хn=2+(-1)n
N), например: хn=2+(-1)n 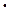
 , т.е.{1; 2,50; 1,67; 2,25; 1,80,...}:
, т.е.{1; 2,50; 1,67; 2,25; 1,80,...}:

Легко заметить, что при возрастании n члены последовательности все ближе подходят к значению А=2. Если вокруг этого значения выделить какую-то область радиусом e (e-окрестность), то при некотором n xn войдет в эту окрестность и уже не выйдет из нее, какой бы малой она ни была. Это и означает, что А - предел, к которому стремится последовательность хn.
|

Рассмотрим последовательность xn = n, n  N, т. е. {1; 2; 3;... }.
N, т. е. {1; 2; 3;... }.
|

Для последовательности хn=  , n Î N, т.е. {1;
, n Î N, т.е. {1;  ;
;  ;...} при возрастании номера n пределом является А=0, т.е.
;...} при возрастании номера n пределом является А=0, т.е.  . Если предел равен 0, то величина называется бесконечно малой.
. Если предел равен 0, то величина называется бесконечно малой.
Последнее, что отметим: переменная, зависящая от натурального аргумента, может иметь только один предел.
Предел функции
Пусть теперь для некоторой функции у=f(х) процесс таков, что х стремится к числу а. Выясним, к чему стремится функция у. Если двигаться от 0 к точке х=а, то в некоторый момент войдем в e-окрестность числа а. При этом функция (при движении по графику) будет ограничена по оси оY d-окрестностью, увязанной с e-окрестностью по оси оХ, и неизбежно приходит в точку х=а, принимая значение А.
|

|

 2015-10-22
2015-10-22 1402
1402

 .
.  и называют xnбесконечно большой величиной.
и называют xnбесконечно большой величиной.  .
.  . Но где-нибудь рядом предел может быть:
. Но где-нибудь рядом предел может быть:  . Если
. Если  , то функция называется бесконечно большой в точке х=а (вариант
, то функция называется бесконечно большой в точке х=а (вариант  ). Если
). Если 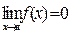 , то функция называется бесконечно малой в точке х=а (вариант
, то функция называется бесконечно малой в точке х=а (вариант 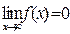 ).
).