2015-10-22
451
Ряд достаточно часто встречающихся в практике пределов по историческим причинам получил название замечательных. Приведем некоторые из них, встречающиеся в практических задачах:
1. 
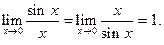2. 
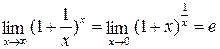, где е =2,718281828...
3. 
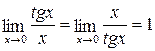. 4. 
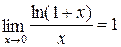. 5.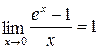 
.
Вычисление пределов
1. Прямая подстановка: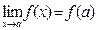 
. Это - наиболее общий прием, который всегда используется первым: 
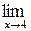(х2 – х + 1) = 42 – 4 + 1 = 13.
2. Упрощение функций. Если при прямой подстановке получается неопределенное выражение типов: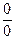 
, 
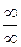и некоторых других, то выделение общего множителя или приведение к замечательным пределам приводят к нужному результату:
= 
= 
= 
= 
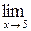
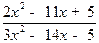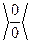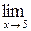
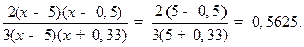
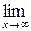
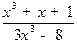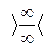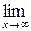
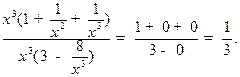
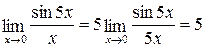
В последнем примере учтено, что, если х 
0, то, очевидно, и 5 х 0 (свойство 3 в разделе 6.3).
