Функции нескольких переменных

Основные понятия

В предыдущих разделах изучались функции одной переменной. Однако многим явлениям присуща многофакторная зависимость. Исследование таких зависимостей потребовало совершенствования математического аппарата, в частности, введения понятия функции нескольких переменных.

Определение. Пусть имеется n переменных величин, и каждому набору их значений (х₁, х₂,..., х_n) из некоторого множества Х соответствует одно вполне определенное значение переменной величины z. Тогда говорят, что задана функция нескольких переменных z=f(х₁,х₂,...,х_n). Например, формула 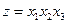задает объем параллелепипеда z как функцию трех переменных: x₁ (длины), х₂ (ширины) и х₃ (высоты).

Переменные х₁, х₂,..., х_n называются независимыми переменными ( или аргументами), z -зависимой переменной, а символ f означает закон соответствия. Множество X называется областью определения функции.

Частный случай функции двух аргументов определяется соотношением z=f(x, у). Основное внимание мы уделим именно этому случаю, т.к. функции трех и более переменных легко вводятся по аналогии.

Линией уровня функции двух переменных z=f(x, у) называется множество точек на плоскости, в которых функция принимает одно и то же значение f(x, y)=С. Число С в этом случае называется уровнем. На рисунке показаны сечения функции двумя плоскостями С₁ и С₂, а также проекции этих сечений на плоскость XoY. Эти проекции изображаются на отдельном чертеже и являются линиями уровня.

Многие примеры линий уровня хорошо известны и привычны. Например, параллели и меридианы на глобусе - это линии уровня функций широты и долготы. Синоптики публикуют карты с изображением изотерм - линий уровня температуры. Построение линий уровня оказывается существенно более легкой задачей, чем построение графиков самих функций.

Все определения и большая часть понятий анализа, определенных ранее для функций одной переменной, может быть перенесена на случай многих переменных без существенных изменений. Несколько увеличивается объем формул, т.к. надо учитывать несколько аргументов. Проиллюстрируем сказанное на примере классического определения предела функции.

Число А называется пределомфункции z=f(x, у) пр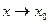и и 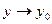(или в точке M₀), если для любого, сколь угодно малого положительного числа 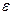, найдется положительное число 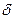, такое, что для всех точек M(х, у), отстоящих от точки M₀(х₀, у₀) на расстояние меньшее, чем 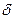, выполняется неравенство .

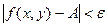Обозначается предел так: .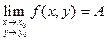

Вычисление пределов функций двух переменных оказывается существенно более трудной задачей по сравнению со случаем одной переменной. Причина заключается в том, что на линии существуют всего два направления, по которым аргумент может стремиться к предельной точке, а именно - справа и слева. На плоскости же таких направлений - бесконечное множество, и пределы функции по разным направлениям могут не совпадать.