Итерационные методы Якоби и Зейделя

Рассмотрим простейшие итерационные методы решения СЛАУ, - методы Якоби (простой итерации) и Зейделя. Будем рассматривать систему

где

(4.2)

- матрица, имеющая обратную матрицу, х = (х₁, х₂, …, х_n)^T, f = (f₁, f₂, …, f_n)^T – соответственно векторы-столбцы неизвестных и правых частей.

Начнем рассмотрение с метода Якоби. Будем считать, что все а_ii ¹ 0, i = 1, 2, …, n, где а_ii – элементы матрицы А, лежащие на главной диагонали. Преобразуем систему (4.1) к виду

(4.3)

В равенстве (4.3) значение суммы считается, как это принято, равным нулю, если значение верхнего предела суммирования меньше значения нижнего предела суммирования.

Далее верхний индекс будет указывать номер итерации (приближения), например,

Зададим произвольным образом начальное приближение номера к = 0, например так

Исходя из равенства (4.3), итерационное равенство (формулу) метода Якоби запишем так

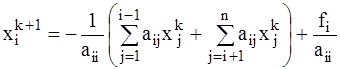, к = 0, 1, 2, …

(4.4)

Окончание итераций определяется:

1) по числу итераций, заданному заранее (максимальному числу итераций);

2) по величине так называемой стабилизации

e > 0 заданное число, близкое к 0;

3) по убыванию нормы вектора невязки на k-ой итерации, где

в заданное число раз по сравнению с нормой вектора начальной невязки , т.е. при выполнении неравенства

Напомним, что в качестве нормы вектора r^k можно взять величины: или k = = 0,1,…

С вычислительной точки зрения способ 3) хотя и более громоздкий, по сравнению со способами 1) и 2), однако, он дает наиболее объективную информацию о погрешности полученного решения.

Идея метода Зейделя состоит в том, чтобы найденные значения использовать для вычисления , усовершенствовав формулу (4.4) так:

(4.6)