Для исследования сходимости итерационных методов, т.е. установления справедливости равенства 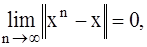 где х – точное решение системы (2.1), удобнее записывать эти методы в матричной, а не в координатной форме.
где х – точное решение системы (2.1), удобнее записывать эти методы в матричной, а не в координатной форме.
Представим матрицу А в виде суммы трех матриц
А = А- + D + A+, где
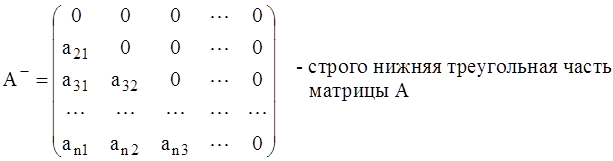

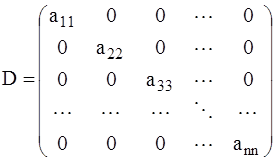 - диагональная часть матрицы А.
- диагональная часть матрицы А.
Очевидно, метод Якоби с использованием введенных обозначений в векторной форме принимает вид
хk+1 = -D-1(А+ + А-)хk + D-1 × f,
где D-1 – матрица, обратная к матрице D


Метод Якоби еще можно записать так
| D(хk+1 – xk) +Axk = f. | (4.7) |
Аналогичным образом из соотношений (4.6) можно получить представление метода Зейделя в векторной форме
| (D + А-)(хk+1 – xk) + Axk = f. | (4.8) |
Далее мы увидим, что векторные равенства (4.7) и (4.8) являются частными случаями так называемой канонической формы одношаговых (двухслойных) итерационных схем вида
 | (4.9) |
где В – квадратная невырожденная матрица n´n, называемая стабилизатором, tk+1 – число, называемое итерационным параметром.
Матрица А называется положительно определенной, если скалярное произведение (Ах, х) > 0 для всех ненулевых векторов, или что то же самое (хТ×, Ах) > 0.
Сформулируем теорему, принадлежащую А.А. Самарскому.
Теорема. Пусть А – симметричная положительно определенная матрица, tk+1 º t > 0, и пусть выполнено неравенство для любого ненулевого вектора х из n-мерного пространства.
((В – 0,5tА)х, х) > 0.
Тогда итерационный метод (4.9) сходится, т.е.

Покажем, как использовать данную теорему для доказательства сходимости, например, метода Зейделя.
Сравнивая (4.8) и (4.9) приходим к равенствам
В = D + А-, t = 1.
Таким образом, если А = АТ и А – положительно определенная матрица, то при условии выполнения неравенства В – 0,5t А > 0, что является краткой формой записи неравенства относительно скалярных произведений
((В – 0,5t А)х, х) > 0, "x Î Rn,
метод Зейделя сходится.
Заметим, что
| В – 0,5t А = В – 0,5 А = D + А- - 0,5(А+ + D + А-) = = 0,5 × D + 0,5(А- - А+). | (4.10) |
Нетрудно проверить, что для любого n-мерного вектора х (х Î Rn)
| ((A- - A+)x, x) = 0. | (4.11) |
C другой стороны, из неравенства (Ах, х) > 0 "x Î Rn вытекает неравенство
| (Dх, х) > 0 | (4.12) |
В самом деле, выберем х = (0, … 0, xi, 0 … 0) где xi ¹ 0. Тогда
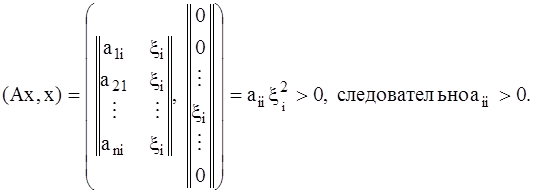
Поскольку i – любое, то все аii > 0, i = 1, 2, …, n. Значит справедливо неравенство (4.12). В силу (4.11) и (4.12) из (4.10) имеем
В – 0,5t А > 0.
 2015-10-22
2015-10-22 2878
2878








