1. Знайти координати вершин, фокусів, півосі і ексцентриситет еліпсів:
1) 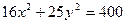 ; 2)
; 2)  ;
;
3) 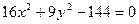 ; 4)
; 4) 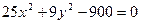 .
.
2. Скласти канонічне рівняння еліпса, фокуси якого на осі ОХ, якщо: 1) 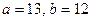 ; 2)
; 2) 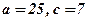 ; 3)
; 3) 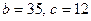 ; 4)
; 4) 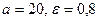 .
.
3. Які з точок А(13, 0), В(5, 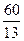 ), С(0, 5), D(
), С(0, 5), D(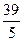 , 4) лежать на еліпсі
, 4) лежать на еліпсі 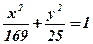 ?
?
4. Скласти канонічне рівняння еліпса, фокуси якого на осі ОХ, якщо він проходить через точки 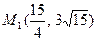 ,
, 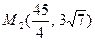 .
.
5. На еліпсі 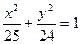 знайти точки з фокальним радіусом
знайти точки з фокальним радіусом 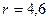 .
.
Вказівка. Використати формули для фокальних радіусів 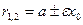
6. Знайти центр, півосі, півфокусну відстань і ексцентриситет для кожного з еліпсів: 1) 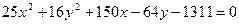 ; 2)
; 2) 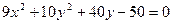 ; 3)
; 3) 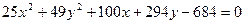 . Записати канонічні рівняння та побудувати графіки.
. Записати канонічні рівняння та побудувати графіки.
7. В еліпс 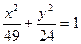 вписано прямокутник, дві протилежні сторони якого проходять через фокуси. Обчислити площу цього прямокутника.
вписано прямокутник, дві протилежні сторони якого проходять через фокуси. Обчислити площу цього прямокутника.
8. Знайти довжину відрізка прямої 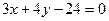 , який міститься у середині еліпса
, який міститься у середині еліпса 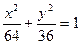 .
.
9. Скласти рівняння спільної хорди еліпса 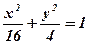 і кола
і кола 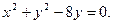
10. Знайти довжину хорди, яка проходить через фокус еліпса 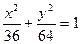 і перпендикулярна великій осі.
і перпендикулярна великій осі.
Відповіді:
1. 1) 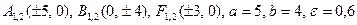 ;
;
2) 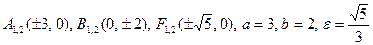 ;
;
3) 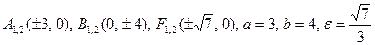 ;
;
4) 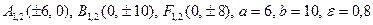 .
.
2. 1) 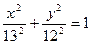 ; 2)
; 2) 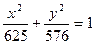 ; 3)
; 3) 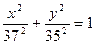 ; 4)
; 4) 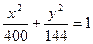 .
.
3. Всі. 4. 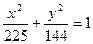 . 5.
. 5. 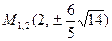 ,
, 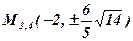 .
.
6. 1) 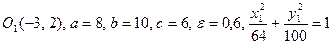 ;
;
2) 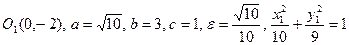 ;
;
3) 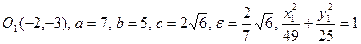 .
.
7. 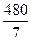 . 8. 10. 9.
. 8. 10. 9. 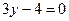 . 10. 9.
. 10. 9.
Гіпербола
Означення. Гіперболою називається множина точок площини, різниця відстаней яких від двох заданих точок, фокусів, є величина стала і дорівнює 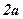 .
.
По аналогії з еліпсом фокуси розміщуємо в точках 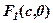 ,
,
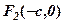 (див. рис. 25-4).
(див. рис. 25-4).
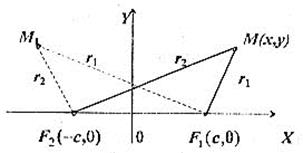
Рис. 25-4.
Оскільки, як видно з рисунка, можуть бути випадки 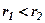 і
і 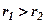 , то згідно означення
, то згідно означення 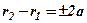 .
.
Відомо, що в трикутнику різниця двох сторін менша третьої сторони, тому, наприклад, з 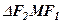 маємо
маємо
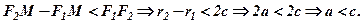
Отже, для гіперболи 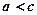 .
.
Далі запишемо значення виразів 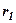 і
і 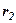 через координати точок
через координати точок
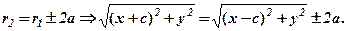
Піднесемо до квадрата обидві частини і після подальших перетворень знайдемо
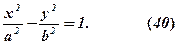
Пропонуємо завершити самостійно 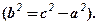

Гіпербола симетрична відносно координатних осей, тому, як і для еліпса, досить побудувати її графік в першій чверті, де 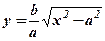 . Область визначення для першої чверті
. Область визначення для першої чверті 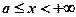 .
.
При 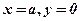 маємо одну із вершин гіперболи
маємо одну із вершин гіперболи 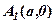 . Друга вершина
. Друга вершина 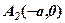 . Якщо
. Якщо 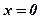 , то із (40)
, то із (40) 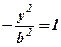 , – дійсних коренів немає. Говорять, що
, – дійсних коренів немає. Говорять, що 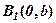 і
і 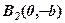 – уявні вершини гіперболи. Із співвідношення
– уявні вершини гіперболи. Із співвідношення 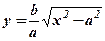 випливає, що при досить великих значеннях
випливає, що при досить великих значеннях 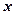 має місце наближена рівність
має місце наближена рівність 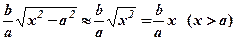 . Тому пряма
. Тому пряма 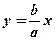 є лінією, відстань між якою і відповідною точкою гіперболи прямує до нуля при
є лінією, відстань між якою і відповідною точкою гіперболи прямує до нуля при  .
.
Пряма 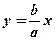 називається асимптотою гіперболи. Згідно з симетрією існує ще одна асимптота
називається асимптотою гіперболи. Згідно з симетрією існує ще одна асимптота 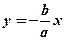 .
.
Для побудови гіперболи необхідно відкласти на координатних осях відрізки довжиною 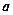 на
на 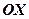 по обидва боки від точки
по обидва боки від точки 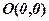 і аналогічно відкласти
і аналогічно відкласти 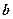 по
по 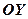 .
.
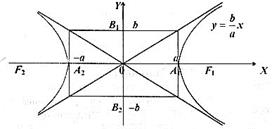
Рис. 26.
Після цього побудувати прямокутник зі сторонами паралельними координатним осям (див. рис. 26). Діагоналі прямокутника є асимптотами гіперболи. Через вершину 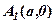 в першій чверті проводимо вітку гіперболи, яка асимптотично наближається до прямої
в першій чверті проводимо вітку гіперболи, яка асимптотично наближається до прямої
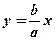 . Інші вітки будуємо симетрично відносно
. Інші вітки будуємо симетрично відносно 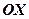 і
і 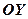 .
.
Ексцентриситет гіперболи 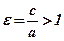 , бо
, бо 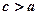 . Якщо величину
. Якщо величину 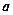 зафіксувати, а
зафіксувати, а  збільшувати, то при цьому збільшується
збільшувати, то при цьому збільшується 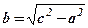 , тому гіперболи будуть відхилятись від
, тому гіперболи будуть відхилятись від 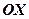 , гіпербола буде розпрямлятись. При зменшені
, гіпербола буде розпрямлятись. При зменшені  буде зменшуватись
буде зменшуватись 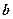 , вітки гіперболи будуть наближатись до
, вітки гіперболи будуть наближатись до 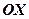 . У випадку, коли
. У випадку, коли 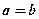 , асимптотами будуть бісектриси координатних кутів,
, асимптотами будуть бісектриси координатних кутів,
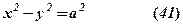
– рівнобічна гіпербола.
Приклади
Побудувати гіперболи
1. 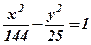 2.
2. 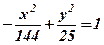 . (Див. рис. 27).
. (Див. рис. 27).
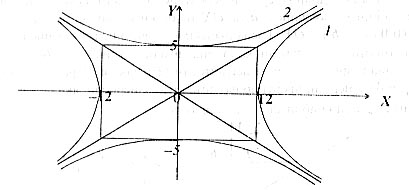
Рис.27.
Перша з гіпербол перетимає вісь 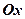 , друга – вісь Oy. Кожна з наведених гіпербол по відношенню до іншої називається спряжною.
, друга – вісь Oy. Кожна з наведених гіпербол по відношенню до іншої називається спряжною.
Рівняння спряжених гіпербол відрізняються протилежними знаками перед змінними в канонічних рівняннях.
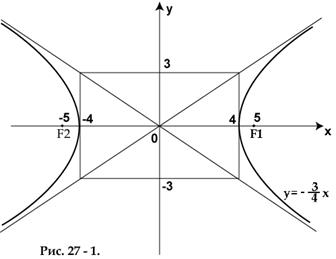
Задача 1. Знайти осі, вершини, фокуси, ексцентриситет і рівняння асимптот гіперболи
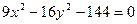 .
.
Побудувати гіперболу та її асимптоти.
Розв’язання. Зведемо рівняння гіперболи до канонічного вигляду 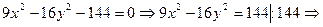
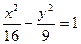 .
.
 |
Порівнюючи дане рівняння з канонічним (див. рівняння (40)) знаходимо
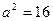 ,
, 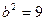 ,
, 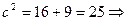
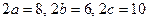 . Вершини
. Вершини 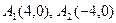 , фокуси
, фокуси 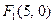 і
і 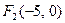 . Ексцентриситет
. Ексцентриситет 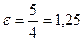 ; асимптоти
; асимптоти 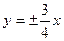 . Будуємо гіперболу (див. рис. 27-1)
. Будуємо гіперболу (див. рис. 27-1)  2015-10-22
2015-10-22 739
739








