Задачі для самостійного розв’язання

1. Знайти координати фокуса і записати рівняння директриси для поданих парабол: 1) ; 2) ; 3) ; 4) .

2. Скласти канонічне рівняння параболи, якщо відомо, що:

а) парабола має фокус і вершину ;

б) парабола симетрична відносно осі абсцис і проходить через точки і ;

в) парабола симетрична відносно осі ординат і проходить через точки і

3. Рівняння директриси параболи . Скласти канонічне рівняння цієї параболи, якщо її вершина в точці . Знайти координати фокуса.

4. На параболі взята точка А(х,у), яка знаходиться від директриси на відстані . Знайти відстань цієї точки від вершини параболи.

5. Знайти фокальний радіус точки В параболи 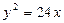, якщо її абсциса дорівнює 8.

6. Знайти точки перетину параболи з прямими: а) 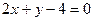; б) ; в) .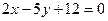

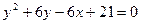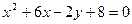7. Знайти координати вершини і фокуса, скласти рівняння осі і директриси кожної із поданих парабол: а) ; б) ; в) ; г) .

8. Вісь симетрії параболи паралельна осі ординат, а рівняння директриси . Скласти рівняння параболи, якщо вона перетинає вісь ОХ в точках (-5, 0) і (11, 0).

9. Через фокус параболи проведені дві прямі, одна з яких складає з віссю ОХ кут , а друга - . Точки перетину цих прямих з параболою послідовно з’єднані між собою. Знайти площу утвореного чотирикутника.

10. Діаметр кругової параболічної антени 60см, глибина її 7,5. На якій відстані від вершини параболи необхідно поставити уловлювач сигналів, щоб відбиті сигнали від супутника перетинались у цій точці (вважається, що сигнали, які напрямлені на антену від супутника йдуть паралельно осі антени).

11. Тіло, кинуте під кутом до горизонту, описало дугу параболи і упало на відстані 32м від початкового положення. Знайти параметр параболічної траєкторії та записати рівняння, якщо найбільша висота досягнута тілом, дорівнює 12м.

Відповіді: 1. 1) ; 2) ; 3) ; 4) . 2. а) ; б) ; в) .

3. . 4. . 5. 14.

6. а) ; б) ; в) . 7. а) ; б) ; в) ; г) . 8. або . 9. . 10. 30. 11.

Конічні перетини

Нехай задана кругова конічна поверхня, необмежена в обидві сторони від вершини. Внаслідок різних перетинів цієї поверхні і площини 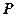можна отримати криві другого порядку (див. рис. 30).

Рис. 30.

1. Якщо площина - осі конічної поверхні, але не проходить через її вершину, то в перетині буде коло .

2. Площина - одній з твірних, тоді в перетині матимемо параболу .

3. Площина 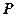перетинає конічну поверхню під кутом до її осі , але жодній з твірних, тоді в перетині буде еліпс .

4. 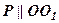, в перетині - гіпербола .

Вироджені випадки:

5. і проходить через вершину конічної поверхні, в перетині є точка .

6. Площина проходить через вісь , в перетині пара прямих, що перетинаються, наприклад, і .

Першим, хто розглядав криві другого порядку, як конічні перетини був древньогрецький математик Аполлоній (прибл. 262 – 190 роки до н.е.). Його праця “Конічні перетини” мала великий вплив на розвиток науки нових часів – астрономії, механіки, оптики; із його положень виходили французькі математики Р.Декарт (1596 – 1650) і П.Ферма (1601 – 1665) при створенні аналітичної геометрії.