Перетворення координат

Одна і та сама лінія в різних системах координат записується різними рівняннями. Часто виникає необхідність переходу від однієї системи координат (“старої”) до іншої (“нової”), як правило з метою отримання простішого рівняння даної кривої в новій системі координат. Формули перетворення виражають зв’язок між новими і старими координатами точки. До них відносяться формули паралельного перенесення координатних осей та формули повороту осей.

І. Паралельне перенесення координатних осей

Позначимо через 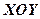стару систему координат, а через – нову, де положення нового початку координат в системі 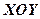(див. рис. 31).

Рис. 31.

З рис. 31 бачимо, що старі координати виражаються через нові :

Звідки

– формули переходу від старих координат до нових при паралельному перенесенні.

При спрощенні кривих другого порядку за допомогою паралельного перенесення використовують спосіб виділення повного квадрата. Розглянемо на прикладі параболи

Позначимо , , отримаємо

Введемо нові координати тоді в новій системі рівняння набуде вигляду (див. рис. 32).

Рис. 32.

Приклади.

1. Спростити рівняння, та побудувати криву

.

Розв’язання. Виділимо повні квадрати відносно 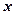і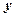

При заміні маємо

– еліпс, , початок нової системи має координати Побудову в новій системі див. на рис. 33.

Рис. 33.

2. Спростити рівняння і побудувати графік кривої

.

Розв’язання. Спочатку згрупуємо відносно змінної х і змінної y

виділимо повні квадрати

Замінимо: одержимо

- гіпербола відносно системи , де

Задачі для самостійного розв’язання

1. Паралельним перенесенням звести до канонічного вигляду (із вказанням нового початку координат) подані нижче рівняння:

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

9) ;

10) .

Відповіді: 1) ;

2) ; 3) ;

4) ; 5) ;

6) ; 7) ;

8) ; 9) ;

10) .