Алгебраїчна форма к.ч

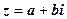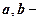В алгебраїчній формі к.ч.мають вигляд , де дійсні числа; число називається дійсною, а – уявною частиною к.ч.; позначення: ; символ формально визначається рівністю 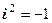і називається уявною одиницею.

Два к.ч. називаються рівними, якщо відповідно рівні їх дійсні та уявні частини.

Основні операції над к.ч. в алгебраїчній формі введені в §§4.4,4.5,4.6.

Надалі домовимось вирази і т.п. вважати к.ч., записаними в алгебраїчній формі, отже, і т.п. набуватимуть тільки дійсних значеннь.

Нехай дано число 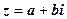. Якщо , то дійсне число: ; якщо , то 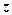називається чисто уявним числом: .

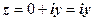Приклад. Розв’язати рівняння ; де дійсні числа.

Розв¢язання. З рівності к.ч. випливає: . Розв’язуючи цю систему, одержимо .

Спряжені к.ч.

Числа 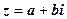і називаються спряженими. Таким чином, якщо і – спряжені числа, то і .

Очевидно, якщо дійсне число, то ; якщо 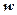– чисто уявне число, то 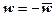. Навпаки, якщо і 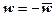, то відповідно 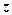і 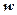- дійсне і чисто уявне числа.

Приклади.

1) Якщо , то .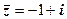

2) Безпосередньо перевіряється тотожність .

Модуль к.ч.

Модулем числа називається невід’ємне число .

Модуль дійсного числа дорівнює його абсолютній величині. Справді, якщо , то .

Приклади.

1) .

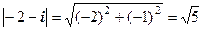2)

3) .

4) Показати, що модулі спряжених чисел рівні.

Розв¢язання. Досить обчислити модулі спряжених чисел