Вычисление определителя

ОСНОВНЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОЙ АЛГЕБРЫ

Метод Гаусса

Вычисление определителя

Пусть задана квадратная матрица

А = 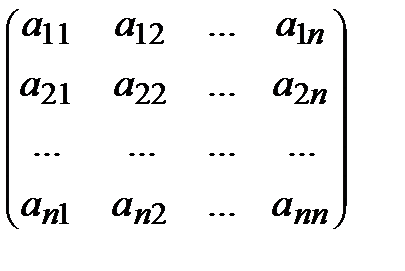. (1)

Предположим, что а ₁₁ ≠ 0. Разделим первую строку матрицы (1) на элемент а ₁₁, который называют ведущим для первого шага. Затем умножаем последовательно полученную строку на а_i ₁ (i = 2,3, …, n) и вычитаем ее из оставшихся строк (i = 2,3, …, n) матрицы (1). В результате все элементы первого столбца, за исключением первого элемента, станут равными нулю, и вместо матрицы (1) получаем эквивалентную ей матрицу

А ⁽¹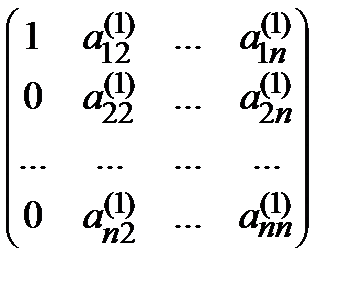⁾ = . (2)

С матрицей (2) поступаем аналогично, но без учета первой матрицы, т.е. преобразуемой теперь является матрица

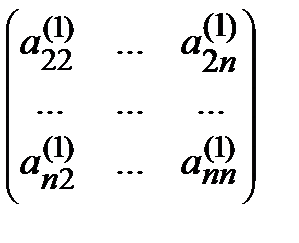После второго шага получаем матрицу, в которой нулевыми элементами будут все элементы первого столбца, за исключением первого элемента, и все элементы второго столбца, за исключением первого и второго элементов. Продолжая описанный процесс, после n -го шага придем к следующей матрице:

А ⁽ ⁿ 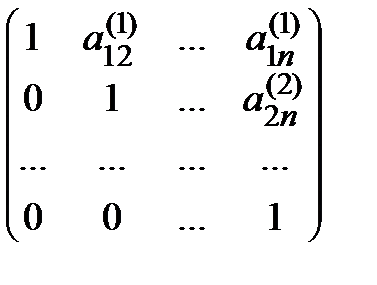⁾ = , (3)

эквивалентной исходной матрице (1).

Заметим, что в данном алгоритме метода Гаусса:

М ₁ = 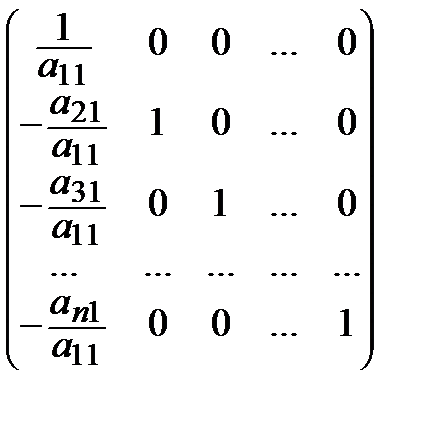, L ₁ = = ,

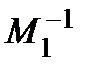А ⁽¹⁾ = .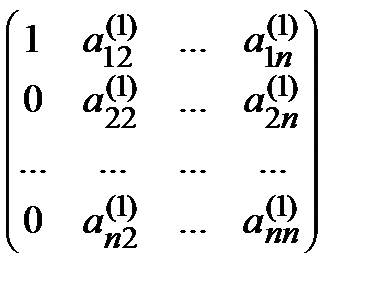

Аналогично можно записать и последующие M_i, A ⁽ ⁱ ⁾ (i = 2, 3, …, n), причем в описанной схеме

М_n = 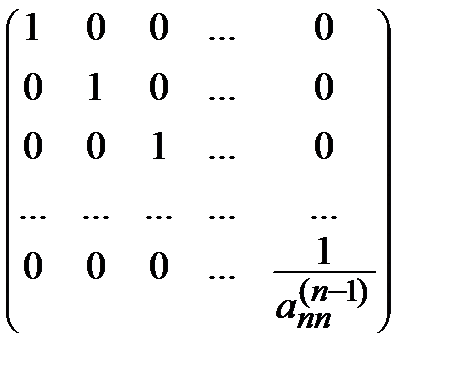, А ⁽ ⁿ ⁾ = ,

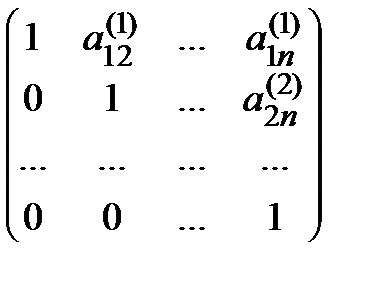L = 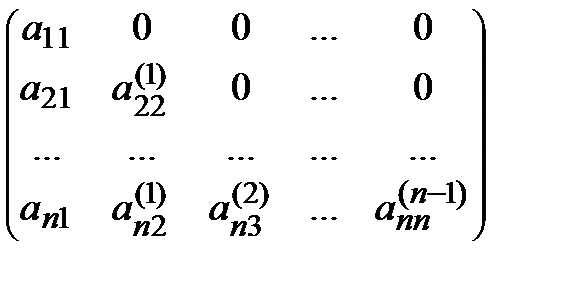и А = L А ⁽ ⁿ ⁾. (4)

Так как известно, что определитель произведения двух квадратных матриц равен произведению определителей перемножаемых матриц, то из полученного разложения (4) следует:

det A = det L · det А ⁽ⁿ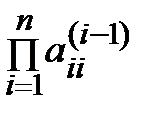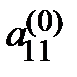⁾ = , = a ₁₁.