Решение системы линейных уравнений

Метод Гаусса для решения системы уравнений

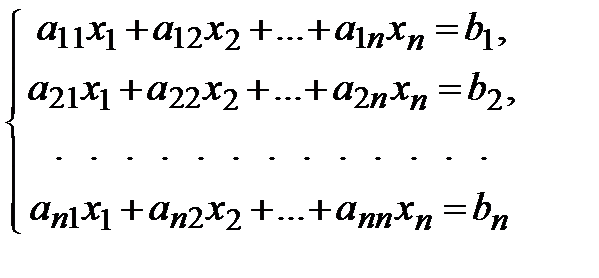(5)

может быть реализован, например, следующим образом: система (5) в матричной записи имеет вид

АХ = В,

где

А = 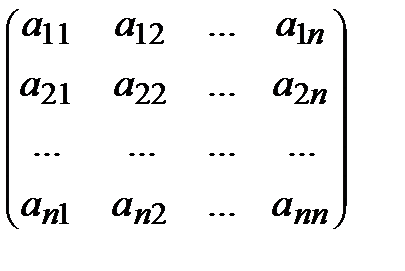– матрица системы, Х = 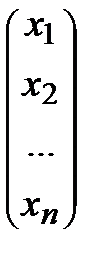– вектор-столбец неизвестных, В = 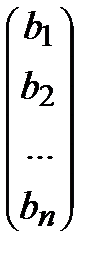– вектор-столбец свободных членов.

Расширенная матрица системы (5)

(A | B) = (A | B)⁽⁰⁾ =

с помощью гауссовых преобразований приводится к эквивалентной матрице

(A | B)^{( n )} = ,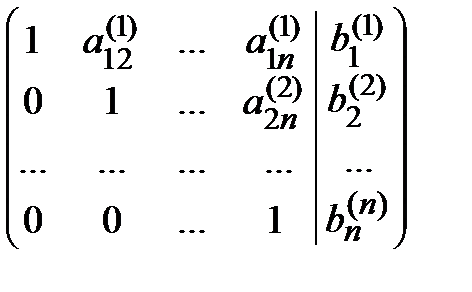

которая соответствует приведенной системе уравнений

(6)

эквивалентной исходной.

Преобразование системы (5) в систему (6) называется прямым ходом, а решение треугольной системы (6) – обратным. Вычислительные формулы этой схемы имеют следующий вид.

Прямой ход, s -й шаг (s = 1, 2, …, n)

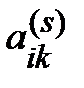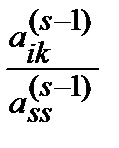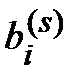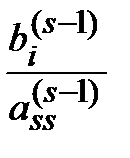= , = (i = s; k = s, s + 1, …, n);

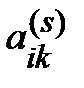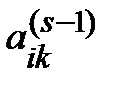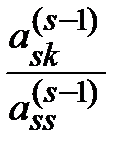
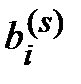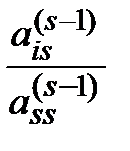
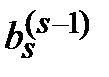= – , = – (i = s +1, s +2, …, n; k = s, s +1, …, n).

Обратный ход осуществляется по формуле:

x_i = 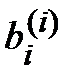– 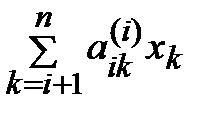(i = n, n – 1, …, 1).