Метод скалярных произведений

Когда матрица А симметричная А = А^Т, для вычисления

максимального собственного значения следует использовать метод скалярных произведений.

Вычислительная схема метода реализуется по формулам

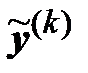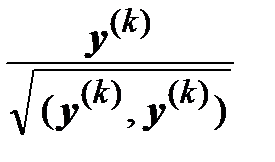= , у ^{( k +1)} = A 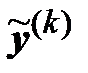, μ ^{( k +1)} = .

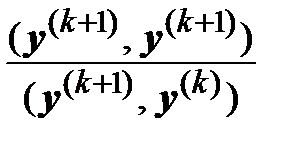Этот же метод можно использовать для вычисления минимального собственного значения матрицы А. В этом случае вычисления производятся по формулам

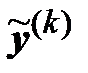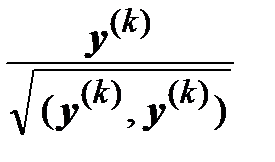= , A у ^{( k +1)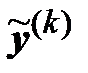} = , μ ^{( k +1)} = .

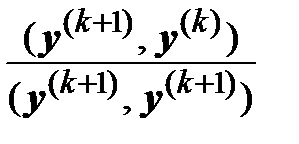Для вычисления приближения у ^{( k +1)} к собственному вектору v ⁽¹⁾ приходится решать систему линейных алгебраических уравнений. Это можно сделать, например, методом Гаусса.