y"+py+qy = 0
(р и q постоянны) в зависимости от корней
характеристического уравнения k2+ pk + q = 0
| Характер корней к1 и к2 характеристического уравнения | Вид общего решения |
| Корни к1 и к2 действительные и различные |  |
| Корни равные: к1 и к2 | у-(  + +  ) )  |
Корни комплексные: к1=  к2= к2=  |  |
Характер частного решения z
неоднородного уравнения у" + ру' + qу = f(х)
(р и q постоянны) в зависимости от правой части f(х)
| Правая часть f(x) | Случаи |   |
 (a,m постоянные) (a,m постоянные) | 1.  , 2. , 2.  . a) . a)  , b) , b)  . . | z=A 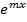 , z=A , z=A  , z=A , z=A  . . |
 (M, N, (M, N,  постоянны) постоянны) | 1. 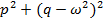 ≠0, 2. ≠0, 2.  | z=Acos 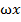 +Bsin +Bsin  z=x(Acos z=x(Acos 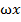 +Bsin +Bsin 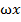 ) ) |
 (a, b, c постоянны) (a, b, c постоянны) | 1. q≠0, 2. q=0, p≠0. | z= A  +Bx+C, z= x(A +Bx+C, z= x(A  +Bx+C) +Bx+C) |
Задание 1: Вычислить пределы
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Задание 2:Найти производные указанных функций
 | |
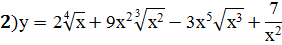 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 |
Задание 3:Найти точки экстремума функции
 |  |
 | 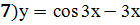 |
 |  |
 |  |
 | 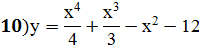 |
 2015-10-22
2015-10-22 778
778








