Интегрирование по частям

Интегрируя обе части равенства d(uv)=udv+vdu, получим

∫ d(uv)= ∫ udv +∫ vdu; uv= ∫ udv+ ∫ vdu,

Откуда

∫udv=uv-∫vdu

С помощью этой формулы вычисление интеграла ∫ udv сводится к вычислению интеграла∫ vdu, если последний окажется проще исходного.

Пример: найти следующие интегралы:

1) 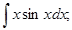2) ; 3) .

1) Положим u=x, dv=sinxdx; тогда du=dx, ∫dv=∫sinxdx, т.е. v=-cosx. Используя формулу (11.14), получим

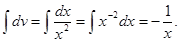2) Положим u =ln x, ; тогда , По формуле (11.14) получим

3) Положим тогда .

По формуле (11.14) получим

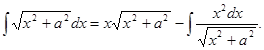
В числителе подынтегральной функции последнего интеграла прибавим и вычтем а ² и представим этот интеграл в виде суммы двух интегралов:

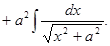
Последний интеграл находим по формуле (11.11):

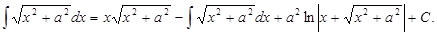
Перенеся из правой части в левую, получим

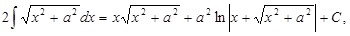
Или окончательно