Определенный интеграл и его непосредственное вычисление

Пусть функция f(x) определена на отрезке a≤x≤b. Разобьем этот отрезок на n частей точками a<x­₀<x₁<x₂<…<x_n=b, выберем на каждом элементарном отрезке x_k-1≤x≤x_k произвольную точку ζ_kи обозначим через ∆ x_k длину каждого такого отрезка. Интегральной суммой для функции f(x) на отрезке a≤x≤b называется сумма вида

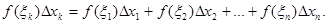
Определенным интегралом от функции f(x) на отрезке a≤x≤b называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:

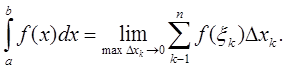
Для любой функции f(x), непрерывной на отрезке a≤x≤b, всегда существует определенный интеграл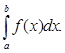

Для вычисления определенного интеграла от функции f(x) в том случае, когда можно найти соответствующий неопределенный интеграл F(x), служит формула Ньютона – Лейбница:

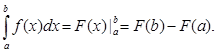
Пример: вычислить следующие интегралы:

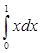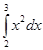1) ; 2) ; 3)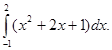

По формуле Ньютона – Лейбница получаем:

1) ;

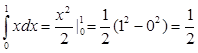2) ;

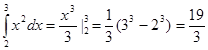3)

.
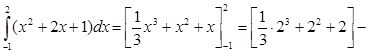
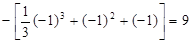ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛОВ

1)Вычислить площадь криволинейной трапеции, ограниченной осью Оx, прямыми x = -1, у = 2 и параболой у = 9 - .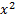

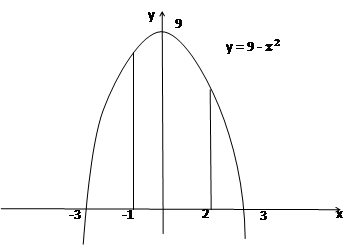Построим график функции у = 9 - 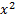и изобразим данную трапецию

Искомая площадь S равна интегралу

.

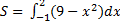По формуле Ньютона – Лейбница находим

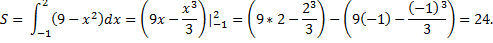
КОМПЛЕКСНЫЕ ЧИСЛА

Комплексными числами называют числа вида a+bi, где aи b– действительные числа, а число i, определяемое равенством 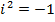, называется мнимой единицей, если для этих чисел понятия равенства и действия сложения и умножения определены следующим образом:

1) Два комплексных числа 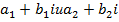называются равными, если ;

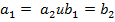2) Суммой двух комплексных чисел 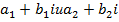называется комплексное число ;

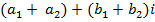3) Произведением двух комплексных чисел 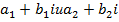называется комплексное число .

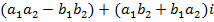ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ, ЗАДАННЫМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ.

Над комплексными числами производится такие же действия, как и над действительными числами. Действия сложения и умножения даны в определении комплексного числа.

Рассматривая вычитание и деление комплексных чисел как действия, обратные соответственно сложению и умножению, получаем правила вычитания и деления комплексных чисел:

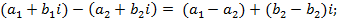
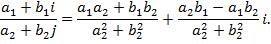
Выполнить действия: 1) (4+2i)+(1+5i); 2) (3 + 5i) – (6 + 3i).

1) По правилу сложения комплексных чисел получим

(4 + 2i) + (1 + 5i) = (4 + 1) + (2 + 5)i = 5 + 7i.

2) По правилу вычитания комплексных чисел получим

(3 + 5i) – (6 + 3i) = (3 - 6) + (5 - 3)i = - 3 + 2i.

Сложение (вычитание) комплексных чисел сводится к сложению (вычитанию) векторов, изображающих эти числа.