Интегрирование путем подведения под знак дифференциала

Все формулы таблицы основных интегралов справедливы, когда переменная интегрирования не является независимой, а представляет функцию от некоторой другой переменной: .

Тогда или .

Пример4. Вычислить интеграл .

Решение. Так как ,

то = .

Здесь мы применили формулу 1 таблицы интегралов.

Пример5. Вычислить интеграл .

Решение. Заметим, что 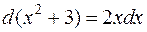, тогда имеем:

= .