Интегрирование по частям в неопределенном интеграле

Теорема. Если функци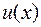и и дифференцируемы на интервале 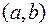, то .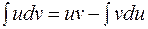

Эта формула называется формулой интегрирования по частям. Она позволяет свести вычисление интеграла 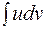к вычислению интеграла 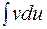, который может оказаться более простым.

Метод интегрирования по частям применяется при вычислении следующих интегралов:

А) 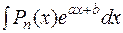, , , где 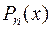- многочлен степени n. В этих интегралах за 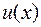принимается 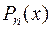и интегрируется по частям n раз.

В) , , , , .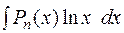

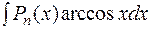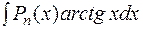В этих интегралах за принимается .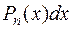

Пример8. Вычислить .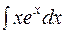

Решение. Положим 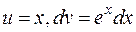, тогда ,

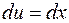и по формуле интегрирования по частям получаем:

= .

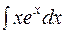Пример9. Вычислить .

Решение. Положим .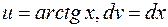

Отсюда . Используя формулу интегрирования по частям, имеем:

= .

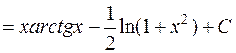Пример10. Вычислить .

Решение. Примем , тогда

. Окончательно получаем:

= .

Пример11. Вычислить .

Решение. Сделаем предварительные преобразования:

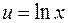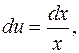
, отсюда

= .